题目内容
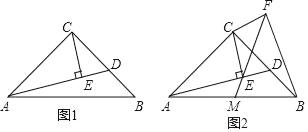
【题目】在等腰Rt△ABC中,∠ACB=90°,AC=BC,点D是边BC上任意一点,连接AD,过点C作CE⊥AD于点E.
(1)如图1,若∠BAD=15°,且CE=1,求线段BD的长;
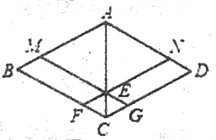
(2)如图2,过点C作CF⊥CE,且CF=CE,连接FE并延长交AB于点M,连接BF,求证:AM=BM.
【答案】(1) 2﹣![]() ;(2)见解析
;(2)见解析
【解析】分析:(1)先求得:∠CAE=45°-15°=30°,根据直角三角形30°角的性质可得AC=2CE=2,再得∠ECD=90°-60°=30°,设ED=x,则CD=2x,利用勾股定理得:![]() x=1,求得x的值,可得BD的长;
x=1,求得x的值,可得BD的长;
(2)如图2,连接CM,先证明△ACE≌△BCF,则∠BFC=∠AEC=90°,证明C、M、B、F四点共圆,则∠BCM=∠MFB=45°,由等腰三角形三线合一的性质可得AM=BM.
详解:(1)∵∠ACB=90°,AC=BC,
∴∠CAB=45°,
∵∠BAD=15°,
∴∠CAE=45°﹣15°=30°,
Rt△ACE中,CE=1,
∴AC=2CE=2,
Rt△CED中,∠ECD=90°﹣60°=30°,
∴CD=2ED,
设ED=x,则CD=2x,
∴CE=![]() x,
x,
∴![]() x=1,
x=1,
x=![]() ,
,
∴CD=2x=![]() ,
,
∴BD=BC﹣CD=AC﹣CD=2﹣![]() ;
;
(2)如图2,连接CM,
∵∠ACB=∠ECF=90°,
∴∠ACE=∠BCF,
∵AC=BC,CE=CF,
∴△ACE≌△BCF,
∴∠BFC=∠AEC=90°,
∵∠CFE=45°,
∴∠MFB=45°,
∵∠CFM=∠CBA=45°,
∴C、M、B、F四点共圆,
∴∠BCM=∠MFB=45°,
∴∠ACM=∠BCM=45°,
∵AC=BC,
∴AM=BM.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目