题目内容
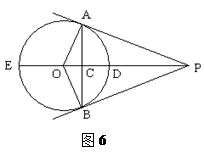
如图,两个同心圆的圆心是O,大圆的半径为13,小圆的半径为5,AD是大圆的直径.大圆的弦AB,BE分别与小圆相切于点C,F.AD,BE相交于点G,连接BD.

(1)求BD 的长;
(2)求∠ABE+2∠D的度数;
(3)求 的值.
的值.

(1)求BD 的长;
(2)求∠ABE+2∠D的度数;
(3)求
 的值.
的值.(1)10
(2)180°
(3)
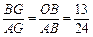
解: (1)连接OC.
∵AB是小圆的切线,C是切点,
∴OC⊥AB,
∴C是AB的中点. …………………1分
∵AD是大圆的直径,
∴O是AD的中点.
∴OC是△ABD的中位线.
∴BD="2OC=10. " ………………………2分
(2)由(1)知C是AB的中点.
同理F是BE的中点.
由切线长定理得BC=BF.
∴BA="BE. " ………………………………3分
∴∠BAE=∠E.
∵∠E=∠D, ………………………………………………………………4分
∴∠ABE+2∠D=∠ABE+∠E+∠BAE="180º. " …………………………5分
(3)在Rt△OCB中,
∵OB="13, " OC=5,
∴BC="12. " ……………………………………………………………6分
由(2)知∠OBG=∠OBC=∠OAC.
∵∠BGO=∠AGB,
∴△BGO∽△AGB. ……………………………………………………7分
∴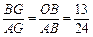 . ……………………………………8分
. ……………………………………8分
∵AB是小圆的切线,C是切点,
∴OC⊥AB,
∴C是AB的中点. …………………1分
∵AD是大圆的直径,
∴O是AD的中点.
∴OC是△ABD的中位线.
∴BD="2OC=10. " ………………………2分
(2)由(1)知C是AB的中点.
同理F是BE的中点.
由切线长定理得BC=BF.
∴BA="BE. " ………………………………3分
∴∠BAE=∠E.
∵∠E=∠D, ………………………………………………………………4分
∴∠ABE+2∠D=∠ABE+∠E+∠BAE="180º. " …………………………5分
(3)在Rt△OCB中,
∵OB="13, " OC=5,
∴BC="12. " ……………………………………………………………6分
由(2)知∠OBG=∠OBC=∠OAC.
∵∠BGO=∠AGB,
∴△BGO∽△AGB. ……………………………………………………7分
∴
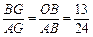 . ……………………………………8分
. ……………………………………8分
练习册系列答案
 能力评价系列答案
能力评价系列答案 唐印文化课时测评系列答案
唐印文化课时测评系列答案
相关题目
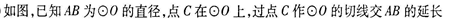

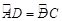 ,则∠DAC的度数是
,则∠DAC的度数是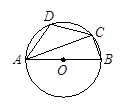
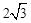 ,则扇形OCED的面积等于( ).
,则扇形OCED的面积等于( ).
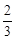 π B.
π B.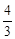 π C.
π C.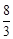 π D.
π D.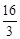 π
π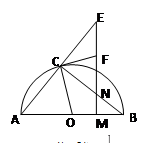
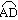 与
与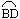 是否相等?说明理由;
是否相等?说明理由;

 cm
cm cm
cm