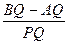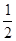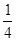题目内容
（本小题满分10分）
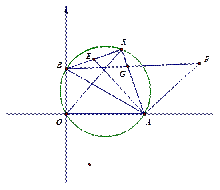
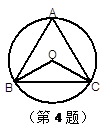
如图，直线AB经过⊙O上的点C，并且OA=OB，CA=CB，⊙O交直线OB于E、D，连接EC、CD．
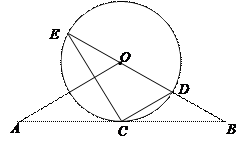
（1）求证：直线AB是⊙O的切线；
（2）试猜想BC，BD，BE三者之间的等量关系，并加以证明
如图，直线AB经过⊙O上的点C，并且OA=OB，CA=CB，⊙O交直线OB于E、D，连接EC、CD．
（1）求证：直线AB是⊙O的切线；
（2）试猜想BC，BD，BE三者之间的等量关系，并加以证明
（1）证明略
（2）证明略
解：（1）证明：如图，连接OC．
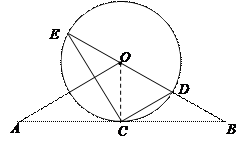
∵OA=OB，CA=CB，
∴OC⊥AB．
∴AB是⊙O的切线．
（2）BC 2=BD·BE．
∵ED是直径，∴∠ECD=90°．
∴∠E +∠EDC=90°．
又∵∠BCD +∠OCD=90°，∠OCD =∠ODC，
∴∠BCD =∠E．
又∵∠CBD =∠EBC，∴△BCD∽△BEC．
∴
．
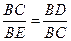∴BC2=BD·BE．
∵OA=OB，CA=CB，
∴OC⊥AB．
∴AB是⊙O的切线．
（2）BC 2=BD·BE．
∵ED是直径，∴∠ECD=90°．
∴∠E +∠EDC=90°．
又∵∠BCD +∠OCD=90°，∠OCD =∠ODC，
∴∠BCD =∠E．
又∵∠CBD =∠EBC，∴△BCD∽△BEC．
∴
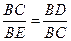．∴BC2=BD·BE．
练习册系列答案
相关题目
的值．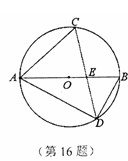
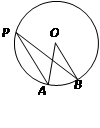
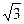，O）、(0，2)，P是△AOB外接圆上的一点，且∠AOP=45°，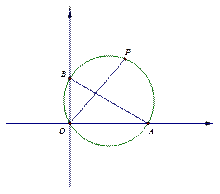
；
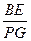