题目内容
【题目】如图,在一次数学活动课上,张明用10个边长为1的小正方形搭成了一个几何体,然后他请王亮用其他同样的小正方体在旁边再搭一个几何体,使王亮所搭几何体恰好可以和张明所搭几何体拼成一个无缝隙的大长方体(不改变张明所搭几何体的形状),那么王亮至少还需要______个小立方体,王亮所搭几何体的表面积为______.
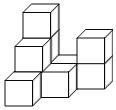
【答案】17 48
【解析】
最小的大正方体是由小方块组成的3×3×3的大正方体,据此可得王亮至少需要的小立方体的个数.根据题意得到题中堆积体的俯视图,并进行标数(地图标数法),即可得出王亮所搭几何体的表面积.
解:由题可知,最小的大正方体是由小方块组成的3×3×3的大正方体,
所以按照张明的要求搭几何体,王亮至少需要27﹣10=17个小立方体.
根据题意得到题中堆积体的俯视图,并进行标数(地图标数法):
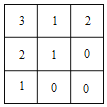
由上图的俯视图可知,能将其补充为完整的3×3×3的大正方体的剩余部分的俯视图为:
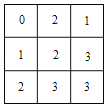
由此可得,王亮所做堆积体的三视图,主、左、俯三视图面积皆为8,
所以王亮所搭几何体的表面积为(8+8+8)×2=48,
故答案为:17,48.

【题目】某校为了解七年级学生的体重情况,随机抽取了七年级m名学生进行调查,将抽取学生的体重情况绘制如下不完整的频数分布表和扇形统计图.
组别 | 体重(千克) | 人数 |
A | 37.5≤x<42.5 | 10 |
B | 42.5≤x<47.5 | n |
C | 47.5≤x<52.5 | 40 |
D | 52.5≤x<57.5 | 20 |
E | 57.5≤x<62.5 | 10 |

请根据图表信息回答下列问题:
(1)填空:①m=_____,②n=_____,③在扇形统计图中,C组所在扇形的圆心角的度数等于_______度;
(2)若把每组中各个体重值用这组数据的中间值代替(例如:A组数据中间值为40千克),则被调查学生的平均体重是多少千克?
(3)如果该校七年级有1000名学生,请估算七年级体重低于47.5千克的学生大约有多少人?