题目内容
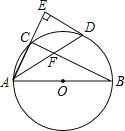
【题目】如图，在Rt△ABC中，∠ACB＝90°，点D在AB上，以AD为直径的⊙O与边BC相切于点E，与边AC相交于点G，且
，连接GO并延长交⊙O于点F，连接BF．
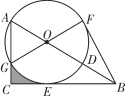
（1）求证：AO＝AG；
（2）求证：BF是⊙O的切线；
（3）若BD＝6，求图形中阴影部分的面积．
【答案】（1）见解析；（2）见解析；（3）S阴影＝
－6π．
【解析】
（1）先利用切线的性质判断出
，再用平行线结合弧相等判断出
，即可得出结论；
（2）先判断出
是等边三角形，进而得出
，进而判断出
，得出
，得出
，即可得出结论；
（3）先判断出
，进而得出
，建立方程
，继而求出
，
，
，
，再判断出
是等边三角形，得出
，进而利用根据勾股定理求出
，即可得出结论．
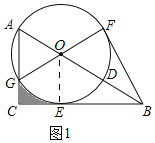
解：（1）证明：如图1，连接
，
与
相切于点
，
，
，
，
，
，
，
，
，
；
（2）由（1）知，
，
，
，
是等边三角形，
，
，
由（1）知，
，
，
，
，
，
，
，
，
是
的半径，
是的切线；
（3）如图2，连接
，
，
，
，
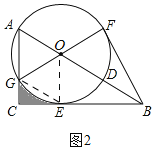
设的半径为
，
，
，
，
，
，
，
，
由（1）知，，
，
是等边三角形，
，
根据勾股定理得，
，
．
练习册系列答案
相关题目
【题目】在水果销售旺季，某水果店购进一优质水果，进价为20元/千克，售价不低于20元/千克，且不超过32元/千克，根据销售情况，发现该水果一天的销售量y（千克）与该天的售价x（元/千克）满足如下表所示的一次函数关系．
销售量y（千克） | … | 34.8 | 32 | 29.6 | 28 | … |
售价x（元/千克） | … | 22.6 | 24 | 25.2 | 26 | … |
（1）某天这种水果的售价为23.5元/千克，求当天该水果的销售量．
（2）如果某天销售这种水果获利150元，那么该天水果的售价为多少元？
