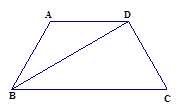
题目内容
如图,在矩形ABCD中,AC与BD相交于O,∠COD=60°,点E是BC边上的动点,连结DE,OE.
(1)求证:△COD是等边三角形;
(2)如图1,当DE平分∠ADC时,试证明OC=EC,并求出∠DOE的度数;

(3)如图2,当DE平分∠BDC时,试证明 .
.
(1)求证:△COD是等边三角形;
(2)如图1,当DE平分∠ADC时,试证明OC=EC,并求出∠DOE的度数;

(3)如图2,当DE平分∠BDC时,试证明
 .
.
(1)根据矩形的性质结合∠COD=60°即可证得结论;(2)135°;(3)根据等边三角形的性质结合DE平分∠BDC可得∠BDE的度数,再根据矩形的性质可得△EBD是等腰三角形,最后根据等腰三角形三线合一的性质即可证得结论.
试题分析:(1)根据矩形的性质结合∠COD=60°即可证得结论;
(2)根据矩形的性质结合DE平分∠ADC可得△DEC是等腰直角三角形,再结合(1)的结论可得OC=EC,∠OCE的度数,最后根据等腰三角形的性质即可求得结果;
(3)根据等边三角形的性质结合DE平分∠BDC可得∠BDE的度数,再根据矩形的性质可得△EBD是等腰三角形,再根据等腰三角形三线合一的性质即可证得结论.
(1)
 ,
,  ,
, ,
,又
 ,
,  ;
;(2)
 ,
,  .
. ,
, ,
, ,
, .
. ,
, ,
, ,
, ,
,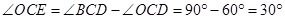 ,
, ,
, ,
, ;
;(3)
 ,
,  .
. ,
, .
. ,
, ,
, ,
,  ,
,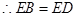 ,
, ,
, ,
, ,
, ,
, .
.点评:解答本题的关键是熟练掌握矩形的对角线相等且互相平分,有一个角是60°的等腰三角形是等边三角形.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
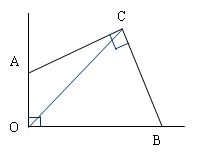
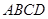 中,
中,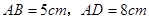 ,
,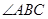 的平分线交
的平分线交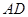 于点
于点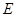 ,交
,交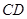 的延长线于点
的延长线于点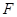 ,那么
,那么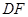 =
= 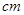
 有3个有效数字;
有3个有效数字; 、
、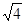 、
、 为边长能组成一个直角三角形
为边长能组成一个直角三角形 的对角线
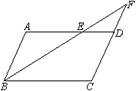
的对角线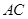 和
和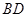 相交于点
相交于点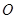 ,过点
,过点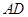 和
和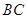 于点E、F,AB=2,BC=4,则图中阴影部分的面积为 .
于点E、F,AB=2,BC=4,则图中阴影部分的面积为 .