题目内容
【题目】用代入消元法解下列方程
(1)![]() (2)
(2) ![]()
(3)![]() (4)
(4)![]()
(5)![]() (6)
(6)![]()
【答案】(1)![]() ;(2)
;(2)![]() ;(3)
;(3)![]() ;(4)
;(4)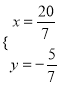 ;(5)
;(5)![]() ;(6)
;(6) .
.
【解析】试题分析:(1) 把②代入①即可求出y,把y的值代入②即可求出x;
(2)把①代入②即可求出x, 把x的值代入①即可求出y.
(3)把①变形得到y=2x-5,再代入②得到x的值,再把x的值代入y=2x-5求得y的值.
(4)把①变形得到x=5+3y,再代入②得到y的值,再把y的值代入x=5+3y求得x的值.
(5)把①代入②即可求出x, 把x的值代入①即可求出y.
(6)把②变形得到p=5-4q,再代入①得到q的值,再把q的值代入p=5-4q求得p的值.
试题解析:
(1) ![]()
把②代入①得:3y+12y=0,
解得:y=1,
把y=1代入②得:x+2=0,
x=2,
即方程组的解为![]() .
.
(2)![]()
将①代入②,
(x3)2x=5,
x=8,
把x=8代入①,
y=11,
∴方程组的解为![]() .
.
(3)![]()
由①得,y=2x-5 ③
把③代入②得x+2x-5=1
解得x=2
把x=2代入①得2×2-y=5
解得y=-1
∴方程组的解为![]() .
.
(4) ![]()
由①得,x=5+3y,③
把③代入②得2(5+3y)+y=5,
解得y=![]() ,
,
代入①得,x3×(57)=5,
解得x=![]() .
.
故原方程组的解为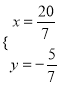 .
.
(5) ![]()
把①代入②得:2x+3(x-3)=6,
解得:x=3,
把x=3代入①得:y=0,
即方程组的解为![]() .
.
(6)![]()
由②得,p=5-4q,③
把③代入①得2(5-4q)-3q=13,
解得![]() ,
,
代入③得,p=5-4×(![]() ),
),
解得![]() .
.
故原方程组的解为 .
.

练习册系列答案
 云南师大附小一线名师提优作业系列答案
云南师大附小一线名师提优作业系列答案 冲刺100分单元优化练考卷系列答案
冲刺100分单元优化练考卷系列答案
相关题目