题目内容
【题目】如图,在平面直角坐标系中, A,B,C 为坐标轴上的三点,且OA=OB=OC=4,过点A 的直线AD 交BC 于点D,交y 轴于点G,△ABD 的面积为8.过点C 作CE⊥AD,交AB 交于F,垂足为E.
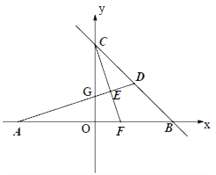
(1)求D 点的坐标;
(2)求证:OF=OG;
(3)在第一象限内是否存在点P,使得△CFP 为等腰直角三角形?若存在,请求出点P 的坐标,若不存在,请说明理由。
【答案】(1)D(2,2);(2)OG=OF=![]() ;(3)P(4,
;(3)P(4, ![]() )、(
)、(![]() ,
, ![]() )或(
)或(![]() ,
, ![]() ).
).
【解析】试题分析:
(1) 过点D作AB的垂线DM,则DM是△ABD的高. 根据已知条件容易求得线段AB的长,根据三角形的面积公式,可以得到线段DM的长,即点D的纵坐标. 利用已知条件易知△BOC是等腰直角三角形,从而可知△BMD也是等腰直角三角形. 利用等腰直角三角形的性质可知线段BM的长,进而获得点D的横坐标.
(2) 利用“同角的余角相等”可以得到∠EGC=∠OFC,利用对顶角关系易得∠OGA=∠OFC. 利用已知条件和上述结论可以证明△AOG与△COF全等,进而证明OF=OG.
(3) 由已知条件可知,当△PCF的三个内角分别等于90°时均存在满足题意的等腰直角三角形. 因此,本小题应该对这三种情况分别进行讨论. 根据题意画出各个情况的示意图. 当∠PCF=90°时,过点P作y轴的垂线PN. 通过全等三角形可以证明PN=CO,NC=OF. 因为已知线段CO的长,只要求得线段OF的长就可以写出点P的坐标. 要求线段OF的长就是要求线段OG的长. 利用△AOG与△AMD的相似关系求得线段OG的长,从而写出点P的坐标. 当∠CFP=90°时,过点P作x轴的垂线PH. 利用已知条件可以证明△FHP与△COF全等,从而利用全等三角形的性质和线段OF与OC的长写出点P的坐标. 当∠CPF=90°时,过点P作x轴的垂线PQ,过点P作y轴的垂线PR. 利用已知条件可以证明△CRP与△FQP全等,从而可知四边形OQPR是正方形. 利用线段FQ,OF与线段OC的数量关系可以求得线段FQ的长,进而获得线段PQ的长. 利用这些条件即可写出点P的坐标.
试题解析:
(1) 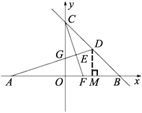
如图,过点D作DM⊥OB,垂足为M.
∵OA=OB=4,
∴AB=OA+OB=4+4=8.
∵△ABD的面积为8,即![]() ,
,
∴DM=2.
∵OB=OC,
∴在Rt△BOC中,∠OBC=45°,
∴在Rt△BMD中,BM=DM=2.
∴OM=OB-BM=4-2=2.
∴点D的坐标为(2, 2).
(2) 证明:∵CE⊥AD,
∴在Rt△CEG中,∠EGC+∠GCE=90°,即∠EGC+∠OCF=90°,
∵在Rt△COF中,∠OFC+∠OCF=90°,
∴∠EGC=∠OFC,
∴∠OGA=∠OFC,
∵在△AOG和△COF中,
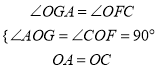 ,
,
∴△AOG≌△COF (AAS).
∴OG=OF,即OF=OG.
(3) 根据题意,分别对下面三种情况进行讨论.
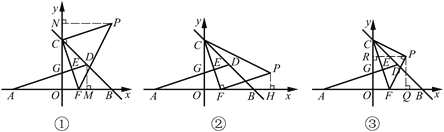
①∠PCF=90°,CF=CP (如图①).
过点D作DM⊥OB,垂足为M. 过点P作PN⊥OC,垂足为N.
∵∠PCN+∠OCF=180°-∠PCF=180°-90°=90°,
又∵在Rt△COF中,∠CFO+∠OCF=90°,
∴∠PCN=∠CFO.
∵在△PNC和△COF中,
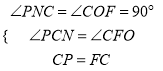 ,
,
∴△PNC≌△COF (AAS).
∴PN=CO=4,NC=OF.
∵DM⊥OB,
∴OG∥DM,
∴△AOG∽△AMD,
∴![]() .
.
∵DM=2,AO=4,AM=AO+OM=4+2=6,
∴OG=![]() ,
,
∴NC=OF=OG=![]() .
.
∴ON=OC+NC=4+![]() =
=![]() .
.
∴点P的坐标为(4, ![]() ).
).
②∠CFP=90°,CF=PF (如图②).
过点P作PH⊥OB,垂足为H.
∵∠HFP+∠CFO=180°-∠CFP=180°-90°=90°,
又∵在Rt△COF中,∠OCF+∠CFO=90°,
∴∠HFP=∠OCF.
∵在△FHP和△COF中,
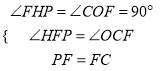 ,
,
∴△FHP≌△COF (AAS).
∴PH=FO=![]() ,FH=CO=4.
,FH=CO=4.
∴OH=OF+FH=![]() +4=
+4=![]() .
.
∴点P的坐标为(![]() ,
,![]() ).
).
③∠CPF=90°,PF=PC (如图③).
过点P作PQ⊥OB,垂足为Q. 过点P作PR⊥OC,垂足为R.
∵∠CPR+∠FPR=∠CPF=90°,
又∵∠FPQ+∠FPR=∠QPR=90°,
∴∠CPR=∠FPQ.
∵在△CRP和△FQP中,
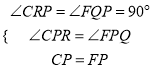 ,
,
∴△CRP≌△FQP (AAS).
∴CR=FQ,PR=PQ.
∵PR=PQ=OQ=OR.
∴OC=CR+OR=FQ+OQ=FQ+(OF+FQ)=2FQ+OF.
∴2FQ+![]() =4.
=4.
∴FQ=![]() .
.
∴PQ=OQ=OF+FQ=![]() +
+![]() =
=![]() .
.
∴点P的坐标为(![]() ,
,![]() ).
).
综上所述,点P的坐标为(4, ![]() ),(
),(![]() ,
,![]() )或(
)或(![]() ,
,![]() ).
).