题目内容
【题目】如图,点A(0,8),点B(4,0),连接AB,点M,N分别是OA,AB的中点,在射线MN上有一动点P.若△ABP是直角三角形,则点P的坐标是__.
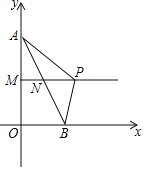
【答案】(2![]() +2,4)或(12,4).
+2,4)或(12,4).
【解析】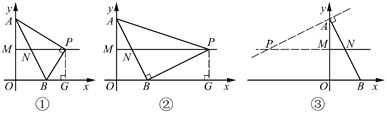
如图,∠APB=90°,∠ABP=90°,∠BAP=90°均可以使△ABP是直角三角形,故本题应该对这三种情况分别进行讨论.
(1) ∠APB=90°,如图①.
过点P作PG⊥OB,垂足为G.
∵点A的坐标为(0, 8),点B的坐标为(4, 0),
∴OA=8,OB=4.
∴在Rt△AOB中, ![]() .
.
∵点M,N分别是OA,AB的中点,
∴MN∥OB, ![]() ,
, ![]() .
.
∵MN∥OB,PG⊥OB,
∴PG=OM=4.
设PN=x,则MP=MN+PN=2+x,
∵OG=MP=2+x,
∴BG=OG-OB=2+x-4=x-2.
∵在Rt△AMP中,AP2=AM2+PM2=42+(2+x)2=16+(2+x)2,
在Rt△BGP中,BP2=BG2+PG2=(x-2)2+42=(x-2)2+16,
又∵在Rt△APB中,AB2=AP2+BP2,
∴16+(2+x)2+(x-2)2+16=![]() =80.
=80.
∴x=![]() ,即PN=
,即PN=![]() .
.
∵OG=2+x=![]() ,PG =4.
,PG =4.
∴点P的坐标为(![]() , 4).
, 4).
(2) ∠ABP=90°,如图②.
过点P作PG⊥OB,垂足为G.
设PN=x,则MP=OG=2+x,BG=x-2.
∵![]() ,AM=4,PG=4,
,AM=4,PG=4,
又∵在Rt△AMP中,AP2=16+(2+x)2,
在Rt△BGP中,BP2=(x-2)2+16,
∴在Rt△APB中,AB2=AP2-BP2=16+(2+x)2-[(x-2)2+16]= ![]() =80.
=80.
∴x=10即PN=10.
∵OG=2+x=2+10=12,PG=4.
∴点P的坐标为(12, 4).
(3) ∠BAP=90°,如图③.
由图③可以看出,在此种情况下点P不在射线MN上,不符合题意.
综上所述,点P的坐标为(![]() , 4)或(12, 4).
, 4)或(12, 4).
故本题应填写:(![]() , 4)或(12, 4).
, 4)或(12, 4).

 轻松课堂单元期中期末专题冲刺100分系列答案
轻松课堂单元期中期末专题冲刺100分系列答案