题目内容
【题目】如图,把矩形纸片ABCD沿EF折叠,使点B落在边AD上的点B′处,点A落在点A′处;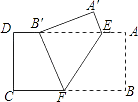
(1)求证:B′E=BF;
(2)设AE=a,AB=b,BF=c,试猜想a,b,c之间的一种关系,并给予证明.
【答案】
(1)证明:由题意得B′F=BF,∠B′FE=∠BFE,
在矩形ABCD中,AD∥BC,
∴∠B′EF=∠BFE,
∴∠B′FE=∠B'EF,
∴B′F=B′E,
∴B′E=BF;
(2)解:a,b,c三者存在的关系是a2+b2=c2.
证明:由(1)知B′E=BF=c,A'E=AE=a,
∵B′E=BF=c,
∴在△A'B'E中,∠A=90°,
∴A'E2+A'B'2=B'E2,
∴a2+b2=c2.
【解析】(1)根据折叠的性质得出B′F=BF,∠B′FE=∠BFE,再根据矩形的性质得出AD∥BC,推出∠B′EF=∠BFE,得出∠B′FE=∠B'EF,从而证得B′F=B′E,即可证得结论。
(2)根据题意可知B′E=BF=c,A'E=AE=a,B′E=BF=c,根据勾股定理的逆定理即可证得结论。
【考点精析】利用勾股定理的概念和矩形的性质对题目进行判断即可得到答案,需要熟知直角三角形两直角边a、b的平方和等于斜边c的平方,即;a2+b2=c2;矩形的四个角都是直角,矩形的对角线相等.

练习册系列答案
相关题目
【题目】某中学八年级的篮球队有10名队员![]() 在“二分球”罚篮投球训练中,这10名员各投篮50次的进球情况如下表:
在“二分球”罚篮投球训练中,这10名员各投篮50次的进球情况如下表:
进球数 | 42 | 32 | 26 | 20 | 19 | 18 |
人数 | 1 | 1 | 2 | 1 | 2 | 3 |
针对这次训练,请解答下列问题:
![]() 求这10名队员进球数的平均数、中位数;
求这10名队员进球数的平均数、中位数;
![]() 求这支球队投篮命中率______;
求这支球队投篮命中率______;
![]() 若队员小亮“二分球”的投篮命中率为
若队员小亮“二分球”的投篮命中率为![]() ,请你分析一下小亮在这支球队中的投篮水平.
,请你分析一下小亮在这支球队中的投篮水平.
![]() 投篮命中率
投篮命中率![]() 进球数
进球数![]() 投篮次数
投篮次数![]()