Question

【题目】如图，在△ABC中，∠ACB= ，D为AC上一点，DE⊥AB于点E，AC=12，BC=5．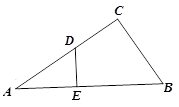

（1）求 的值；
（2）当 时，求 的长．

Answer 1

【答案】
（1）解：解法一：∵DE⊥AB，

∴∠DEA=90°．

∴∠A+∠ADE=90°．

∵∠ACB= ，

∴∠A+∠B=90°．

∴∠ADE=∠B．

在Rt△ABC中，∵AC=12，BC=5，

∴AB=13．

∴ ．

∴

解法二：∵ ，

∴ ．

∵ ，

∴△ ∽△ ．

∴ ．

在Rt△ 中，∵ ，

∴

∴

∴

（2）解：解法一：由（1）得 ，

设 为 ，则 ．

∵ ，

∴ ．

解得 ．

∴ ．

解法二：由（1）可知 △ ∽△ ．

∴

设 ，则 ．

∴ ．

解得 ．

∴ ．

【解析】（1）根据勾股定理求出AB的值，根据同角的余角相等，得到∠ADE=∠B，根据三角函数的定义求出cos∠ADE的值；（2）根据三角函数值直接求出AD的值即可.
【考点精析】利用锐角三角函数的定义和同角三角函数的关系（倒数、平方和商）对题目进行判断即可得到答案，需要熟知锐角A的正弦、余弦、正切、余切都叫做∠A的锐角三角函数；各锐角三角函数之间的关系：平方关系（sin2A+cos2A=1）；倒数关系（tanAtan(90°—A)=1）；弦切关系（tanA=sinA/cosA ）．