题目内容
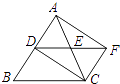
【题目】在△ABC中,已知AB=AC,∠A=36°,AB的垂直平分线MN交AC于D.在下列结论中:①∠C=72°;②BD是∠ABC的平分线;③∠BDC=100°;④△ABD是等腰三角形;⑤AD=BD=BC.正确的有____.(填写序号)
【答案】①②④⑤
【解析】
先根据题意画出图形,再利用垂直平分线的性质,求出各个角的度数即可解题.
解:根据题意作图:

①项,因为AB=AC,∠A=36°,所以∠ABC=∠ACB=![]() (180°-36°)=72°,故符合题意;
(180°-36°)=72°,故符合题意;
②项,因为MN是AB的垂直平分线,所以AD=BD,所以∠A=∠ABD=36°,∠CBD=72°-36°=36°,所以BD是∠ABC的平分线,故符合题意;
③项,∠BDC=180°-72°-36°=72°,故不符合题意;
④项,因为MN是AB的垂直平分线,所以AD=BD,所以△ABD是等腰三角形,故符合题意;
⑤项,从以上已知AD=BD,∠BDC=180°-72°-36°=72°,所以BD=BC,则AD=BD=BC,故符合题意.
故答案为①②④⑤.

 阅读快车系列答案
阅读快车系列答案【题目】小明在超市帮妈妈买回一袋纸杯,他把纸杯整齐地叠放在一起,如图请你根据图中的信息,若小明把100个纸杯整齐叠放在一起时,它的高度约是( )

A.106cmB.110cmC.114cmD.116cm
【题目】如图,把矩形纸片ABCD沿EF折叠,使点B落在边AD上的点B′处,点A落在点A′处;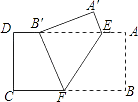
(1)求证:B′E=BF;
(2)设AE=a,AB=b,BF=c,试猜想a,b,c之间的一种关系,并给予证明.
【题目】某中学初三年级的同学参加了一项节能的社会调查活动,为了了解家庭用电的情况,他们随即调查了某地50个家庭一年中生活用电的电费支出情况,并绘制了如下不完整的频数分布表和频数分布直方图(费用取整数,单位:元).
分组/元 | 频数 | 频率 |
1000<x<1200 | 3 | 0.060 |
1200<x<1400 | 12 | 0.240 |
1400<x<1600 | 18 | 0.360 |
1600<x<1800 | a | 0.200 |
1800<x<2000 | 5 | b |
2000<x<2200 | 2 | 0.040 |
合计 | 50 | 1.000 |

请你根据以上提供的信息,解答下列问题:
(1)补全频数分布表a= , b= , 和频数分布直方图;
(2)这50个家庭电费支出的中位数落在哪个组内?
(3)若该地区有3万个家庭,请你估计该地区有多少个一年电费支出低于1400元的家庭?