题目内容
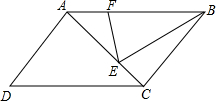
如图，是某个公园ABCDEF，M为AB的中点，N为CD的中点，P为DE的中点，Q为FA的中点，其中游览区APEQ与BNDM的面积和是900平方米，中间的湖水面积为361平方米，其余的部分是草地，则草地的总面积是______平方米．
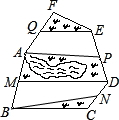
连接AE、AD，BD．
因为M为AB的中点，N为CD的中点，P为DE的中点，Q为FA的中点，
根据一个三角形的中线平分这个三角形的面积，
所以设S△EFQ=S△AQE=a，
S△AEP=S△APD=b，
S△ADM=S△BDM=c，
S△BDN=S△BCN=d．
因为游览区APEQ与BNDM的面积和是900平方米，中间湖水AMDP的面积是361平方米，
即a+b+c+d=900平方米，b+c=361平方米
所以a+d=900-361=539平方米
即草地的总面积S△EFQ+S△BCN=a+d=539平方米．
故答案为：539．
因为M为AB的中点，N为CD的中点，P为DE的中点，Q为FA的中点，
根据一个三角形的中线平分这个三角形的面积，
所以设S△EFQ=S△AQE=a，
S△AEP=S△APD=b，
S△ADM=S△BDM=c，
S△BDN=S△BCN=d．
因为游览区APEQ与BNDM的面积和是900平方米，中间湖水AMDP的面积是361平方米，
即a+b+c+d=900平方米，b+c=361平方米
所以a+d=900-361=539平方米
即草地的总面积S△EFQ+S△BCN=a+d=539平方米．
故答案为：539．
练习册系列答案
开心快乐假期作业暑假作业西安出版社系列答案
相关题目
