��Ŀ����
����Ŀ��Ϊ���������裬�û���ũ�ḻũ���ҵ����������Ͳʵ����磬���Ҿ���ʵ�������������涨ÿ����һ̨�ʵ磬������������Ԫ��������ij�̳����۲ʵ�̨��y��̨���벹�����x��Ԫ��֮�����������ͼ��ʾ��һ�κ�����ϵ�����Ų������x�IJ�������������Ҳ�������ӣ���ÿ̨�ʵ������p��Ԫ������Ӧ���������㣺p=�� ![]() x+110��x��0����
x+110��x��0���� 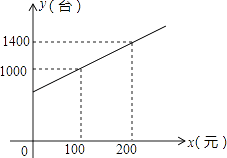
��1����������������ʵʩ��������̳����۲ʵ�̨��y�������������x֮��ĺ�����ϵʽ��
��2��������δ��̨������ʩ֮ǰ�����̳����۲ʵ���������Ϊ����Ԫ��
��3��Ҫʹ���̳����۲ʵ���������������Ӧ��ÿ̨�������x��Ϊ���٣����������������ֵ��
���𰸡�
��1���⣺�������⣬����y=kx+b
����100��1000������200��1400��������ʽ���ã� ![]() ��
��
��� ![]() ��
��
���������ĺ�����ϵʽΪ��y=4x+600
��2���⣺����y=4x+600�У���x=0ʱ��y=600��
�� ![]() �У���x=0ʱ��p=110
�У���x=0ʱ��p=110
��600��110=66000
��������δ��̨������ʩ֮ǰ�����̳����۲ʵ���������Ϊ66000Ԫ
��3���⣺��������ΪWԪ����
W= ![]()
= ![]()
= ![]()
�� ![]() ��
��
��W�������ֵ��
�൱x=200ʱW�����ֵ98000��
������Ӧ��ÿ̨������Ϊ200Ԫʱ���ɻ���������98000Ԫ
����������1���������⣬����y=kx+b������100��1000������200��1400��������ʽ�����ɽ�����⣮��2���ֱ��������̨����ÿ̨�������ɽ�����⣮��3���������κ�����Ȼ�������䷽��ȷ��������ֵ���⣮

 һ����ʦ�����Ծ�ϵ�д�
һ����ʦ�����Ծ�ϵ�д�