题目内容
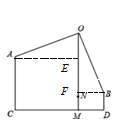
【题目】在一款名为超级玛丽的游戏中,玛丽到达一个高为10米的高台A,利用旗杆顶部的绳索,划过90°到达与高台A水平距离为17米,高为3米的矮台B,

(1)求高台A比矮台B高多少米?
(2)求旗杆的高度OM;
(3)玛丽在荡绳索过程中离地面的最低点的高度MN.
【答案】(1)7米;(2)OM=15m;(3)玛丽在荡绳索过程中离地面的最低点的高度MN为2米.
【解析】试题分析:(1)作差.(2) 作AE⊥OM,BF⊥OM,证明在△AOE和△OBF相似,可以计算出OE+OF长度,最后算出OM长度.(3)利用勾股定理求出半径长度,作差求MN长度.
试题解析:
(1)10-3=7(米).
(2)作AE⊥OM于E,,BF⊥OM与F,
∵∠AOE+∠BOF=∠BOF+∠OBF=90°,
∴∠AOE=∠OBF,
在△AOE和△OBF中,
 ,
,
∴△AOE≌△OBF(AAS),
∴OE=BF,AE=OF,
即OE+OF=AE+BF=CD=17(m)
∵EF=EM﹣FM=AC﹣BD=10﹣3=7(m),
∴2EO+EF=17,
则2EO=10,
所以OE=5m,OF=12m,
所以OM=OF+FM=15m.
(3)由勾股定理得ON=OA=13,
所以MN=15﹣13=2(m).
答:玛丽在荡绳索过程中离地面的最低点的高度MN为2米.

 名校提分一卷通系列答案
名校提分一卷通系列答案 课程达标测试卷闯关100分系列答案
课程达标测试卷闯关100分系列答案 新卷王期末冲刺100分系列答案
新卷王期末冲刺100分系列答案 全能闯关100分系列答案
全能闯关100分系列答案【题目】甲、乙两城市为了解决空气质量污染问题,对城市及其周边的环境污染进行了综合治理.在治理过程中,环保部门每月初对两个城市的空气质量进行监测,连续10个月的空气污染指数如下图所示.其中,空气污染指≤50时,空气质量为优;50<空气污染指数≤100时,空气质量为良;100<空气污染指数≤150时,空气质量为轻微污染.

(1)请填写下表:
平均数 | 方差 | 中位数 | 空气质量为优的次数 | |
甲 | 80 | 1 | ||
乙 | 1060 | 80 |
(2)请回答下面问题:
①从平均数和中位数来分析,甲、乙两个城市的空气质量;
②从平均数和方差来分析,甲、乙两个城市的空气质量变化情况;
③根据折线图上两城市的空气污染指数的走势及优的情况来分析两城市治理环境污染的效果.




