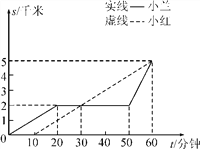
题目内容
【题目】如图,在矩形OABC中,OA=3,OC=5,分别以OA、OC所在直线为x轴、y轴,建立平面直角坐标系,D是边CB上的一个动点(不与C、B重合),反比例函数y=![]() (k>0)的图象经过点D且与边BA交于点E,连接DE.
(k>0)的图象经过点D且与边BA交于点E,连接DE.
(1)连接OE,若△EOA的面积为3,则k=___________;
(2)是否存在点D,使得点B关于DE的对称点在OC上?若存在,求出点D的坐标;若不存在,请说明理由.
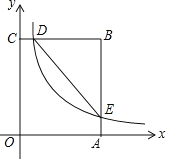
【答案】(1)6;(2)存在,D(![]() ,5).
,5).
【解析】分析:(1)连接OE,根据反比例函数k的几何意义,即可求出k的值.(2)根据矩形的长和宽及反比例函数y=![]() (k>0)表示D和E的坐标,计算tan∠BDE=tan∠CB′B的值相等,所以计算B′C的长,得出D的坐标.
(k>0)表示D和E的坐标,计算tan∠BDE=tan∠CB′B的值相等,所以计算B′C的长,得出D的坐标.
本题解析:
(1)连接OE,如图1,
∵Rt△AOE的面积为3,
∴k=2×3=6.
故答案为:6;
(2)连接DB′,
设D(![]() ,5),E(3,
,5),E(3,![]() ),
),
∴BD=3﹣![]() ,BE=5﹣
,BE=5﹣![]() ,
,
∴tan∠BDE=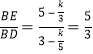 ,
,
∵B与B′关于DE对称,
∴DE是BB′的中垂线,
∴BB′⊥DE,BG=B′G,DB′=BD,
∴∠DGB=90°,
∴∠BDE+∠DBB′=90°,
∠CB′B+∠DBB′=90°,
∴∠BDE=∠CB′B,
∴tan∠BDE=tan∠CB′B=![]() =
=![]() =
=![]() ,
,
∴CB′=![]() ,
,
设CD=x,则BD=B′D=3﹣x,
则![]() ,
,
∴x=![]() ,
,
∴D(![]() ,5).
,5).

练习册系列答案
相关题目