题目内容
【题目】(1)在如图所示的数轴上,把数﹣2, ![]() ,4,﹣
,4,﹣![]() ,2.5表示出来,并用“<“将它们连接起来;
,2.5表示出来,并用“<“将它们连接起来;
(2)假如在原点处放立一挡板(厚度不计),有甲、乙两个小球(忽略球的大小,可看作一点),小球甲从表示数﹣2的点处出发,以1个单位长度/秒的速度沿数轴向左运动;同时小球乙从表示数4的点处出发,以2个单位长度/秒的速度沿数轴向左运动,在碰到挡板后即刻按原来的速度向相反的方向运动,设运动的时间为t(秒).
请从A,B两题中任选一题作答.
A.当t=3时,求甲、乙两小球之间的距离.
B.用含t的代数式表示甲、乙两小球之间的距离.
![]()
【答案】(1)答案见解析(2)A.7;B.0<t≤2时,6-t;t>2时,3t-2.
【解析】试题分析:(1)先将各数表示在数轴上,然后按照数轴上越右的数越大用“<”号连接起来即可;
(2)甲球到原点的距离=甲球运动的路程+OA的长,乙球到原点的距离分两种情况:(Ⅰ)当0<t≤2时,乙球从点B处开始向左运动,一直到原点O,此时OB的长度-乙球运动的路程即为乙球到原点的距离;(Ⅱ)当t>2时,乙球从原点O处开始向右运动,此时乙球运动的路程-OB的长度即为乙球到原点的距离;
A、当t=3时,根据上面的分析进行计算即可得;
B、分0<t≤2与t>2两种情况进行讨论即可得.
试题解析:(1)如图所示:
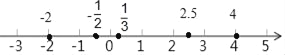
-2<-![]() <
<![]() <2.5<4;
<2.5<4;
(2)∵甲球运动的路程为:1t=t,OA=2,∴甲球与原点的距离为:t+2;
乙球到原点的距离分两种情况:
(Ⅰ)当0<t≤2时,乙球从点B处开始向左运动,一直到原点O,
∵OB=4,乙球运动的路程为:2t=2t,∴乙球到原点的距离为:4-2t;
(Ⅱ)当t>2时,乙球从原点O处开始一直向右运动,此时乙球到原点的距离为:2(t-2)=2t-4;
A、当t=3时,甲、乙两小球之间的距离为:t+2+2t-4=3t-2=7;
B、分两种情况:(Ⅰ)0<t≤2,甲、乙两小球之间的距离为:t+2+4-2t=6-t;
(Ⅱ)t>2,甲、乙两小球之间的距离为:t+2+2t-4=3t-2.

 新题型全程检测期末冲刺100分系列答案
新题型全程检测期末冲刺100分系列答案【题目】2004年4月我国铁路第5次大提速。假设Kl20次空调快速列车的平均速度提速后比提速前提高了44千米/时,提速前的列车时刻表如下:
行驶区间 | 车次 | 起始时刻 | 到站时刻 | 历时 | 全程里程 |
A地—B地 | K120 | 2:00 | 6:00 | 4小时 | 264千米 |
请你根据题目提供的信息,填写提速后的列车时刻表,并写出计算过程。
行驶区间 | 车次 | 起始时刻 | 到站时刻 | 历时 | 全程里程 |
A地—B地 | K120 | 2:00 | 264千米 |