��Ŀ����
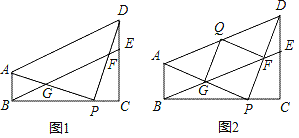
����Ŀ��������ABCD�У���QΪAB����һ�㣬��FΪBC����һ������DQ��DF��QF��
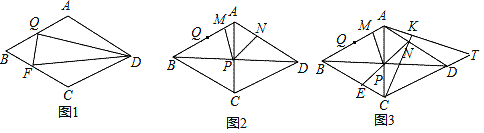
��1����ͼ1������ADQ=��FDQ����FQD=90������֤��AQ=BQ��
��2����ͼ2���ڣ�1���������£���BAD=120�����Խ���AC��BD�ཻ�ڵ�P���Ե�PΪ��������MPN=60�㣬PM��AB���ڵ�M��PN��AD���ڵ�N����֤��DN+QM=AB��
��3����ͼ3���ڣ�1����2���������£��ӳ�NP��BC�ڵ�E���ӳ�CN����K��ʹCK=CA������AK���ӳ���CD���ӳ��߽��ڵ�T����AM��DN=1��5��S�ı���MBEP=12![]() �����߶�DT�ij���
�����߶�DT�ij���
���𰸡���1��֤������������2��֤������������3��DT=4��
��������
��1���������ߣ�֤����FQD�ա�LQD�͡�ALQ�ա�BFQ���ɵý��ۣ�
��2����ͼ2������QP����AQ=BQ��������ֱ��������б�����ߵ����ʵã�PA=PQ�����ԡ�APQ�ǵȱ������Σ�֤����PQM�ա�PAN��ASA������QM=AN������AB=AD=DN+AN������ɵý��ۣ�
��3����ͼ3���������ߣ�����ֱ�ǡ�AMG��ֱ�ǡ�CEH����AM=a����DN=5a�����ݣ�2����AB=DN+QM����AB=8a��֤����PCE�ա�PAN����CE=AN=3a�����ݹ��ɶ�������BP��MG��EH�ij�������S�ı���MBEP=12![]() ���з��̿ɵ�a��ֵ��
���з��̿ɵ�a��ֵ��
��AM=1��AN=3��DN=5��CD=8����C��CI��AD��I����ID=![]() CD=
CD=![]() ��8��4�����ݹ��ɶ�����CN�ij���
��8��4�����ݹ��ɶ�����CN�ij���
��CD�Ͻ�ȡCS��ʹCS=DN=5������AS��֤����ACS�ա�CDN��SAS�����ɵý��ۣ�
֤������1����ͼ1���ֱ��ӳ�FQ��DA����L��
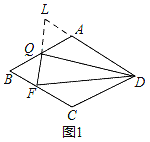
�ߡ�ADQ=��FDQ��DQ=DQ����FQD=��LQD=90�㣬
���FQD�ա�LQD��ASA����
��FQ=LQ��
���ı���ABCD�����Σ�
��LD��BF��
���ALQ=��BFQ����LAQ=��FBQ��
���ALQ�ա�BFQ��
��AQ=BQ��
��2����ͼ2������QP��
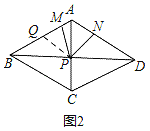
���ı���ABCD��������
���BAP=��DAP��PA=PC��AC��BD��
���APB=��APD=90�㣬
�ߡ�BAD=120�㣬
���BAP=��DAP=60�㣬
���ABP=30�㣬
��PA=![]() AB��
AB��
��AQ=BQ��
��PQ=![]() AB��
AB��
��PA=PQ��
���APQ�ǵȱ������Σ�
���APQ=��PQA=60�㣬
�ߡ�MPN=60�㣬
���APQ=��MPN=60�㣬
���QPM=��APN��
�ߡ�PQM=��PAN=60�㣬
���PQM�ա�PAN��ASA����
��QM=AN��
��AB=AD=DN+AN��
��AB=DN+QM��
��3���⣺��ͼ3������M��MG��AC��G������E��EH��AC��H����AM=a��
��AM��DN=1��5��
��DN=5a��
�ɣ�2��֪��AB=DN+QM��
��AQ=![]() AB��QM=AQ��AM��
AB��QM=AQ��AM��
��5a+![]() AB��a=AB��AB=8a��
AB��a=AB��AB=8a��
���ı���ABCD��������
��AD��BC��
���ABC+��BAD=180�㣬
�ߡ�BAD=120�㣬
���ABC=60�㣬
���ABC�ǵȱ������Σ�
��AC=AB=8a��
��AN=3a��
�ߡ�APN=��CPE��AP=CP����DAC=��BCA=60�㣬
���PCE�ա�PAN��ASA����
��CE=AN=3a��
Rt��BPC�У���CBP=30�㣬BC=8a��
��BP=4![]() a��
a��
ͬ��MG=![]() a��EH=
a��EH=![]() a��
a��
��S�ı���MBEP=S��ABC��S��APM��S��CPE��
��![]() ��
��![]() ��
��![]() =12
=12![]() ��
��
��a2=1��a=1��a=��1��ȥ����
��AM=1��AN=3��DN=5��CD=8��
��C��CI��AD��I��
��ID=![]() =
=![]() ��
��
��NI=ND��ID=5��4=1��
��Rt��CID��CD2=DI2+CI2��
��CI2=CD2��ID2=82��42=48��
��Rt��ICN��CN2=NI2+CI2��
��CN2=1+48=49��
��CN=7��
��CD�Ͻ�ȡCS��ʹCS=DN=5������AS��
��AN=SD=3��
�ߡ�ACS=��CDN=60�㣬AC=CD��
���ACS�ա�CDN��SAS����
���CAS=��DCN��SA=NC=7��
��CA=CK��
���CAK=��CKA��
���SAK=��KTC��
��SA=ST=7��
��DT=7��3=4��