Question

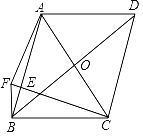
【题目】如图，在ABCD中，对角线AC和BD相交于点O，在AB上有一点E，连接CE，过点B作BC的垂线和CE的延长线交于点F，连接AF，∠ABF=∠FCB，FC=AB，若FB=1，AF=，则BD=_____．

Answer 1

【答案】5

【解析】

作辅助线，构建全等三角形和直角三角形，证明△AGB≌△FBC，得AG=BF=1，BC=BG，在Rt△AFG中利用勾股定理计算FG的长，在Rt△DGB中，根据勾股定理可得BD的长．

解：延长BF、DA交于点G，

∵四边形ABCD是平行四边形，

∴AD∥BC，

∴∠G+∠GBC=180°，

∵BF⊥BC，

∴∠FBC =90°，

∴∠G=90°，

在△AGB和△FBC中，

，

∴△AGB≌△FBC，

∴AG=BF=1，BC=BG，

Rt△AGF中，

∵FG===2，

∴BC=BG=AD=2+1=3，

∴GD=1+3=4，

Rt△DGB中，BD===5，

故答案为：5．