题目内容
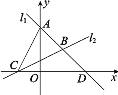
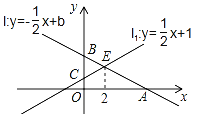
【题目】如图,已知直线l:y=﹣![]() x+b与x轴,y轴的交点分别为A,B,直线l1:y=
x+b与x轴,y轴的交点分别为A,B,直线l1:y=![]() x+1与y轴交于点C,直线l与直线ll的交点为E,且点E的横坐标为2.
x+1与y轴交于点C,直线l与直线ll的交点为E,且点E的横坐标为2.
(1)求实数b的值和点A的坐标;
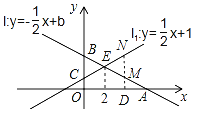
(2)设点D(a,0)为x轴上的动点,过点D作x轴的垂线,分别交直线l与直线ll于点M、N,若以点B、O、M、N为顶点的四边形是平行四边形,求a的值.
【答案】(1)b=3,A(6,0);(2) a的值为5或﹣1
【解析】
(1)将点E的横坐标为2代入y=![]() x+1求出点E的坐标,再代入y=﹣
x+1求出点E的坐标,再代入y=﹣![]() x+b中可求出b的值,然后令﹣
x+b中可求出b的值,然后令﹣![]() x+b=0解之即可得出A点坐标;
x+b=0解之即可得出A点坐标;
(2)由题可知,MN//OB,只需再求出当MN=OB时的a值,即可得出答案.
(1)∵点E在直线l1上,且点E的横坐标为2,
∴点E的坐标为(2,2),
∵点E在直线l上,
∴![]() ,
,
解得:b=3,
∴直线l的解析式为![]() ,
,
当y=0时,有![]() ,
,
解得:x=6,
∴点A的坐标为(6,0);
(2)如图所示,
当x=a时,![]() ,
,![]() ,
,
∴![]() ,
,
当x=0时,yB=3,
∴BO=3.
∵BO∥MN,
∴当MN=BO=3时,以点B、O、M、N为顶点的四边形为平行四边形,
此时|2﹣a |=3,
解得:a=5或a=﹣1.
∴当以点B、O、M、N为顶点的四边形为平行四边形,a的值为5或﹣1.

练习册系列答案
相关题目