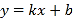题目内容
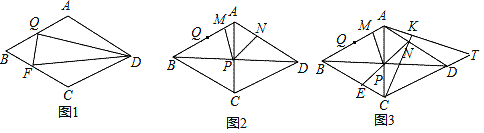
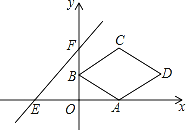
【题目】已知:在四边形ABCD中,∠ABC=∠DCB=90°,点P在BC边上,连接AP和PD,点E在DC边上,连接BE与DP和AP分别交于点F和点G,若AB=PC,BP=DC,∠DFE=45°.
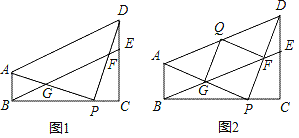
(1)如图1,求证:四边形ABED为平行四边形;
(2)如图2,把△PFG沿FG翻折,得到△QFG(点P与点Q为对应点),点Q在AD上,在不添加任何辅助线的情况下,请直接写出图中所有的平行四边形(不包括平行四边形ABED,但包括特殊的平行四边形).
【答案】(1)证明见解析;(2)四边形AGFQ是平行四边形,四边形QGFD是平行四边形.
【解析】
(1)证明△ABP≌△PCD,可以得出△PAD为等腰直角三角形,得出∠ADP=45°,可得AD∥BE,再证出AB∥DE即可解决问题;
(2)根据平行四边形的判定方法即可判断.
解:(1)∵∠ABC=∠DCB=90°,
∴∠ABC+∠DCB=180°,
∴AB∥CD,
∵AB=PC,BP=DC,
∴△ABP≌△PCD,
∴PA=PD,
∠APD=∠PDC,
∵∠PDC+∠DPC=90°,
∴∠APB+∠DPC=90°,
∴∠APD=90°,
∴△APD是等腰直角三角形,
∴∠ADP=45°,
∵∠DFE=45°,
∴∠ADP=∠DFE,
∴AD∥BE,
∴四边形ABED是平行四边形.
(2)∵∠PGF=∠PAD=45°,∠PFG=∠ADP=45°,
∴△PFG,△FGQ都是等腰直角三角形,
∴四边形PFQG是正方形,
∵∠AGF=135°,∠QFG=∠PFG=45°,
∴∠AGF+∠QFG=180°,
∴AG∥QF,
∵AQ∥FG,
∴四边形AGFQ是平行四边形,
同法可证,四边形QGFD是平行四边形,

练习册系列答案
相关题目