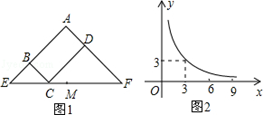
题目内容
如图,在平面直角坐标系中,一次函数 的图象与反比例函数
的图象与反比例函数 的图象在第一象限内交于点
的图象在第一象限内交于点 ,与
,与 轴交于点
轴交于点 ,与
,与 轴交于点
轴交于点 ,
, 。
。

(1)求一次函数和反比例函数的解析式;
(2)若在 轴上存在点
轴上存在点 ,使得
,使得 ,求点
,求点 的坐标。
的坐标。
 的图象与反比例函数
的图象与反比例函数 的图象在第一象限内交于点
的图象在第一象限内交于点 ,与
,与 轴交于点
轴交于点 ,与
,与 轴交于点
轴交于点 ,
, 。
。
(1)求一次函数和反比例函数的解析式;
(2)若在
 轴上存在点
轴上存在点 ,使得
,使得 ,求点
,求点 的坐标。
的坐标。(1) 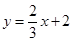 ,
,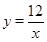 ;(2)P点坐标为(
;(2)P点坐标为(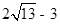 ,0)或(
,0)或(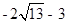 ,0).
,0).
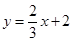 ,
,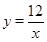 ;(2)P点坐标为(
;(2)P点坐标为(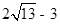 ,0)或(
,0)或(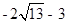 ,0).
,0).试题分析:(1)由一次函数
 可求出C点坐标(0,2),由
可求出C点坐标(0,2),由 可求出B点坐标(-3,0),继而可求出一次函数解析式;因A(3,n)是直线与双曲线的交点,从而可求出n的值,反比例函数解析式可求.
可求出B点坐标(-3,0),继而可求出一次函数解析式;因A(3,n)是直线与双曲线的交点,从而可求出n的值,反比例函数解析式可求.(2)首先计算AB的长,设P(a,0),用含有a的代数式表示BP,由
 可求出a的值,从而求出点
可求出a的值,从而求出点 的坐标.
的坐标.试题解析:(1)在直线
 上,令x=0,则y=2
上,令x=0,则y=2∴C点坐标为(0,2)
在Rt△BCO中,

∴

∴BO=3
∴B点坐标为(-3,0)
∵直线
 经过点B
经过点B∴-3k+2=0
∴k=
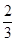
∴一次函数为
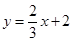
又A(3,n)为直线与双曲线的交点,
∴
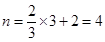
∴A(3,4)
∴
 ,即m=12.
,即m=12.∴反比例函数为
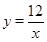 .
.(2)在Rt△ABD中,
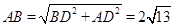
设P点坐标为(a,0)
∴

∴a=
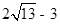 或a=
或a=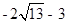
∴P点坐标为(
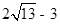 ,0)或(
,0)或(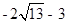 ,0)
,0)考点: 反比函数的综合题.

练习册系列答案
相关题目
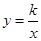 (
(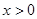 )经过C点,且OB·AC=160,则
)经过C点,且OB·AC=160,则 的值为___________.
的值为___________.
 与
与 ,如果存在函数
,如果存在函数 (
( )则称函数
)则称函数 ,并且其中一个函数满足:当
,并且其中一个函数满足:当 时,
时, 随
随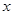 的增大而增大.
的增大而增大. 和
和 的中和函数
的中和函数 的图象和函数
的图象和函数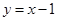 的图象相交于两点,试求当
的图象相交于两点,试求当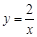 的图象上,第二象限内的点B在反比例函数 y =
的图象上,第二象限内的点B在反比例函数 y = 的图象上,且OA⊥OB,tanA=
的图象上,且OA⊥OB,tanA=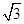 ,则k的值为
,则k的值为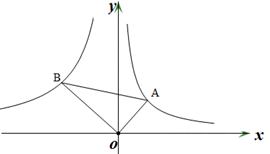
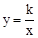
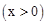 的图象分别交BA,BC于点D,E.当AD:BD=1:3且
的图象分别交BA,BC于点D,E.当AD:BD=1:3且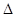 BDE的面积为18时,则
BDE的面积为18时,则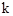 的值是( )
的值是( )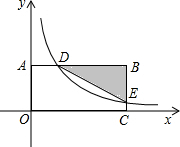
 )、B(1,
)、B(1,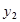 )、C(2,
)、C(2, )是反比例函数
)是反比例函数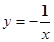 图象上的三个点,则下列结论正确的是( )
图象上的三个点,则下列结论正确的是( )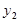
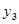 >
> 的图象上的是( )
的图象上的是( ) 的图象在( )
的图象在( )