题目内容
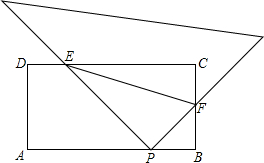
如图，矩形ABCD的边AB上有一点P，且AD=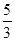
，BP=
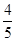，以点P为直角顶点的直角三角形两条直角边分别交线段DC，线段BC于点E，F，连接EF，则tan∠PEF=_______．
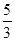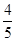，BP=，以点P为直角顶点的直角三角形两条直角边分别交线段DC，线段BC于点E，F，连接EF，则tan∠PEF=_______．
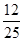
过点E作EM⊥AB于点M，证明△EPM∽△PFB，利用对应边成比例可得出PF：PE的值，继而得出tan∠PEF．
解：过点E作EM⊥AB于点M，
∵∠PEM+∠EPM=90°，∠FPB+∠EPM=90°，
∴∠PEM=∠FPB，
又∵∠EMP=∠PBF=90°，
∴△EPM∽△PFB，
∴
=
=
=．
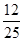∴tan∠PEF==．
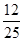故答案为：．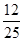
解：过点E作EM⊥AB于点M，
∵∠PEM+∠EPM=90°，∠FPB+∠EPM=90°，
∴∠PEM=∠FPB，
又∵∠EMP=∠PBF=90°，
∴△EPM∽△PFB，
∴
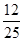===．∴tan∠PEF=
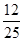=．故答案为：
．
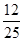练习册系列答案
同步练习强化拓展系列答案
相关题目
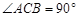，D是边AB的中点，BE⊥CD，垂足为点E，己知AC=6，sinA=
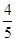．(1) 求线段CD的长；(2)求cos∠DBE的值．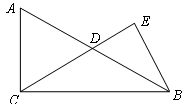
|+
＋（－
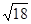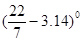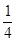）－1
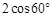的值等于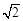
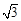
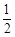
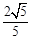
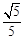
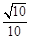
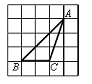
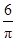cm，一只蚂蚁从点
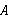爬到点
处吃食， 要爬行的最短路程是（ ）cm．
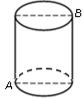
＋(1－
)°＝________．