题目内容
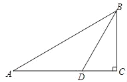
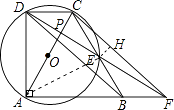
【题目】如图，直角梯形ABCD中，AB∥CD，∠DAB=90°，且∠ABC=60°，AB=BC，△ACD的外接圆⊙O交BC于E点，连接DE并延长，交AC于P点，交AB延长线于F． 
（1）求证：CF=DB；
（2）当AD= 
时，试求E点到CF的距离．
【答案】
（1）证明：连结AE，如图，
∵∠ABC=60°，AB=BC，
∴△ABC为等边三角形，
∵AB∥CD，∠DAB=90°，
∴∠ADC=∠DAB=90°，
∴AC为⊙O的直径，
∴∠AEC=90°，即AE⊥BC，
∴BE=CE，
CD∥BF，
∴∠DCE=∠FBE，
在△DCE和△FBE中，
，
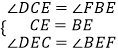∴△DCE≌△FBE（ASA），
∴DE=FE，
∴四边形BDCF为平行四边形，
∴CF=DB
（2）解：作EH⊥CF于H，如图，
∵△ABC为等边三角形，
∴∠BAC=60°，
∴∠DAC=30°，
在Rt△ADC中，AD= 
，
∴DC= 
AD=1，AC=2CD=2，
∴AB=AC=2，BF=CD=1，
∴AF=3，
在Rt△ABD中，BD= 
= 
，
在Rt△ADF中，DF= 
=2 ，
∴CF=BD= ，EF= 
DF= ，
∵AE⊥BC，
∴∠CAE=∠BAE=30°，
∴∠EDC=∠CAE=30°，
而∠DCA=∠BAC=60°，
∴∠DPC=90°，
在Rt△DPC中，DC=1，∠CDP=30°，
∴PC= DC= ，
∵∠HFE=∠PFC，
∴Rt△FHE∽Rt△FPC，
∴ 
，即 
= 
，
∴EH= 
，
即E点到CF的距离为 ．
【解析】（1）连结AE，由∠ABC=60°，AB=BC可判断△ABC为等边三角形，由AB∥CD，∠DAB=90°得∠ADC=∠DAB=90°，则根据圆周角定理可得到AC为⊙O的直径，则∠AEC=90°，即AE⊥BC，根据等边三角形的性质得BE=CE，再证明△DCE≌△FBE，得到DE=FE，于是可判断四边形BDCF为平行四边形，根据平行四边形的性质得CF=DB；（2）作EH⊥CF于H，由△ABC为等边三角形得∠BAC=60°，则∠DAC=30°，在Rt△ADC中，根据含30度的直角三角形三边的关系得DC= AD=1，AC=2CD=2，则AB=AC=2，BF=CD=1，AF=3，然后利用勾股定理计算出BD= ，DF=2 ，所以CF=BD= ，EF= DF= ，接着根据等边三角形的性质由AE⊥BC得∠CAE=∠BAE=30°，根据圆周角定理得∠EDC=∠CAE=30°，而∠DCA=∠BAC=60°，得到∠DPC=90°，在Rt△DPC中，根据含30度的直角三角形三边的关系得PC= DC= ，再证明Rt△FHE∽Rt△FPC，利用相似比可计算出EH．
