题目内容
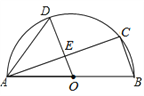
【题目】如图,AB是半圆O的直径,C、D是半圆O上的两点,且OD∥BC,OD与AC交于点E.

(1)若∠B=70°,求弧CD的度数;
(2)若AB=26,DE=8,求AC的长.
【答案】(1)![]() 的度数是70°;(2) AC=24.
的度数是70°;(2) AC=24.
【解析】试题分析:(1)根据圆周角定理可得∠ACB=90°,则可得∠CAB的度数,由OD∥BC,可得∠AOD的度数,又OD=OA,从而可得∠OAD的度数,从而得到∠DAC的度数,继而得到弧CD的度数;
(2)易证OE是△ABC的中位线,由DE的长可得OE的长,利用中位线定理求得BC的长,由勾股定理即可得AC的长.
试题解析:(1)∵AB是直径,∴∠C=90°,∵∠B=70°,∴∠BAC=20°,
∵OD∥BC,∴∠AOD=∠B=70°,又OD=OA,∴∠OAD=55°,
∴∠DAC=35°,∴![]() 的度数是70°;
的度数是70°;
(2)∵AB=26,∴OD=13,又DE=8,∴OE=5,
∵OD∥BC,OA=OB,∴BC=2OE=10,又∵∠C=90°,∴AC=![]() =24.
=24.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目

