题目内容
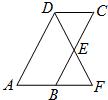25、如图，已知平行四边形ABCD中，点E为BC边的中点，延长DE，AB相交于点F．（1）图中与BF相等的线段有
CD、AB
（写1条）；（2）对于（1）中的结论分别进行证明．
分析：（1）根据全等三角形的性质和平行四边形的性质可得出图中与BF相等的线段；
（2）根据ASA可证△BEF≌△CED，再由全等三角形的对应边相等，可得与BF相等的线段，再由平行四边形的对边相等证明与BF相等的另一条线段．
（2）根据ASA可证△BEF≌△CED，再由全等三角形的对应边相等，可得与BF相等的线段，再由平行四边形的对边相等证明与BF相等的另一条线段．
解答：解：（1）图中与BF相等的线段有CD、AB．
（2）∵点E为BC边的中点，
∴BE=EC．
∵四边形ABCD平行四边形，
∴AB=CD，∠DCB=∠CBF．
又∵∠DEC=∠BEF，
∴△BEF≌△CED．
∴BF=CD=AB．
（2）∵点E为BC边的中点，
∴BE=EC．
∵四边形ABCD平行四边形，
∴AB=CD，∠DCB=∠CBF．
又∵∠DEC=∠BEF，
∴△BEF≌△CED．
∴BF=CD=AB．
点评：解决本题的关键是运用线段中点的定义、全等三角形的性质和平行四边形的性质．
练习册系列答案
相关题目
CD的边长a等于点P，Q间的距离．
如图，已知平行四边形ABCD的对角线AC，BD相交于点O，BD绕点O顺时针旋转交AB，DC于E，F．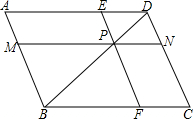
交AB、CD、AD、BC于M、N、E、F，设a=PM•PE，b=PN•PF．
23、如图，已知平行四边形ABCD．
如图，已知平行四边形ABCD，作DE⊥AB，垂足为E，把三角形AED沿AB方向平移AB长个单位长度．