题目内容
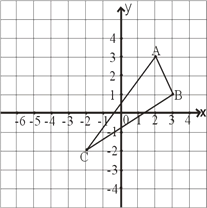
【题目】如图,在长方形ACDF中,AC=DF,点B在CD上,点E在DF上,BC=DE=a,AC=BD=b,AB=BE=c,且AB⊥BE.
(1)用两种不同的方法表示出长方形ACDF的面积S,并探求a,b,c之间的等量关系(需要化简)
(2)请运用(1)中得到的结论,解决下列问题:
①求当c=10,a=6时,求S的值;
②当c﹣b=1,a=5时,求S的值.

【答案】(1)详见解析;(2)①112;②204.
【解析】
(1)方法一可直接求长方形ACDF的面积;方法二可求四个三角形面积的和;根据面积相等化简可得a2+b2=c2;
(2)①根据(1)中结论可求出b=8,然后根据S=ab+b2计算即可;
②根据(1)中结论可求出b=12,然后根据S=ab+b2计算即可.
解:(1)由题意,得
方法一:S1=b(a+b)=ab+b2;
方法二:S2=![]() ab+
ab+![]() ab+
ab+![]() (b﹣a)(b+a)+
(b﹣a)(b+a)+![]() c2=ab+
c2=ab+![]() b2﹣
b2﹣![]() a2+
a2+![]() c2,
c2,
∵S1=S2,
∴ab+b2=ab+![]() b2﹣
b2﹣![]() a2+
a2+![]() c2,
c2,
∴2ab+2b2=2ab+b2﹣a2+c2,
∴a2+b2=c2;
(2)∵a2+b2=c2,且c=10,a=6,
∴b=8,
∴S=ab+b2=6×8+64=112,
答:S的值为112;
②∵a2+b2=c2,
∴a2=c2﹣b2=(c+b)(c﹣b).
又∵c﹣b=1,a=5,
∴c+b=25,
∴b=12,
∴S=ab+b2=5×12+122=204.

练习册系列答案
 培优好卷单元加期末卷系列答案
培优好卷单元加期末卷系列答案
相关题目