题目内容
【题目】如图,已知![]() 的外角
的外角![]() 的平分线交
的平分线交![]() 边的垂直平分线于点
边的垂直平分线于点![]() .
.![]() 于点
于点![]() ,
,![]() 于点
于点![]() .
.
(1)求证:![]()
(2)若![]() ,
,![]() ,求
,求![]() 的长
的长

【答案】(1)见解析;(2)3.
【解析】
(1)连接PB、PC,根据线段垂直平分线的性质得到PB=PC,根据角平分线的性质得到PD=PE,证明Rt△BPD≌Rt△CPE,根据全等三角形的性质可得![]() ;
;
(2)证明Rt△ADP≌Rt△AEP,得到AD=AE,根据题意列出方程,解方程即可.
(1)证明:连接PB、PC,
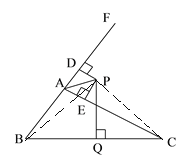
∵PQ是BC边的垂直平分线,
∴PB=PC,
∵AP平分∠DAC,PD⊥AB,PE⊥AC,
∴PD=PE,
在Rt△BPD和Rt△CPE中,![]() ,
,
∴Rt△BPD≌Rt△CPE,
∴BD=CE;
(2)解:在Rt△ADP和Rt△AEP中,![]() ,
,
∴Rt△ADP≌Rt△AEP,
∴AD=AE,
∵BD=CE,![]() ,
,![]() ,
,
∴AD+6=12-AD,
解得,AD=3.

练习册系列答案
相关题目