题目内容
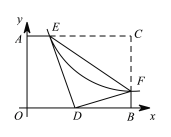
【题目】如图,反比例函数y=![]() (k>0)的图像与矩形AOBC的边AC,BC分别交于点E、F,点C的坐标为(8,6),将△CEF沿EF翻折,C点恰好落在OB上的点D处,则k的值为( )
(k>0)的图像与矩形AOBC的边AC,BC分别交于点E、F,点C的坐标为(8,6),将△CEF沿EF翻折,C点恰好落在OB上的点D处,则k的值为( )
A.![]() B.6C.12D.
B.6C.12D.![]()
【答案】D
【解析】
过点E作EM⊥OB于点M,根据折叠的性质得∠EDF=∠C=90°,EC=ED,CF=DF,易证Rt△EDM∽Rt△DFB;而EC=AC-AE=8-![]() ,CF=BC-BF=6-
,CF=BC-BF=6-![]() ,得到ED=8-
,得到ED=8-![]() ,DF=6-
,DF=6-![]() ,即可得
,即可得![]() 的比值;故可得出EM:DB=ED:DF=4:3,而EM=6,从而求出DB,然后在Rt△DBF中利用勾股定理得到关于k的方程,解方程求出k的值即可得到F点的坐标.
的比值;故可得出EM:DB=ED:DF=4:3,而EM=6,从而求出DB,然后在Rt△DBF中利用勾股定理得到关于k的方程,解方程求出k的值即可得到F点的坐标.
∵将△CEF沿EF对折后,C点恰好落在OB上的D点处,
∴∠EDF=∠C=90°,EC=ED,CF=DF,
∴∠EDM+∠FDB=90°,
过点E作EM⊥OB于点M,
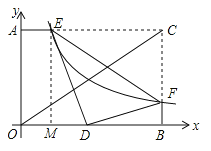
则∠MED +∠EDM=90°,
∴∠MED=∠FDB,
∴Rt△EDM∽Rt△DFB;
又∵EC=AC-AE=8-![]() ,CF=BC-BF=6-
,CF=BC-BF=6-![]() ,
,
∴ED=8-![]() ,DF=6-
,DF=6-![]() ,
,
∴![]() =
=![]() =
=![]() ;
;
∴EM:DB=ED:DF=4:3,而EM=6,
∴DB=![]() ,
,
在Rt△DBF中,DF2=DB2+BF2,即(6-![]() )2=(
)2=(![]() )2+(
)2+(![]() )2,
)2,
解得k=![]() ,
,
故选:D.

练习册系列答案
 一卷搞定系列答案
一卷搞定系列答案 名校作业本系列答案
名校作业本系列答案 轻巧夺冠周测月考直通名校系列答案
轻巧夺冠周测月考直通名校系列答案
相关题目