题目内容
【题目】如图,在菱形ABCD中,对角线AC、BD相交于点O且AC、BD的长(![]() )是方程
)是方程![]() 的两个根.点P从点A出发,以每秒1个单位的速度沿
的两个根.点P从点A出发,以每秒1个单位的速度沿![]() 边A→O→B→A的方向运动,运动时间为t(秒).
边A→O→B→A的方向运动,运动时间为t(秒).

(1)求AC和BD的长;
(2)求当AP恰好平分![]() 时,点P运动时间t的值;
时,点P运动时间t的值;
(3)在运动过程中,是否存在点P,使![]() 是等腰三角形?若存在,请求出运动时间t的值:若不存在,请说明理由.
是等腰三角形?若存在,请求出运动时间t的值:若不存在,请说明理由.
【答案】(1)![]() ,
,![]() ;(2)
;(2)![]() 秒;(3)存在,综上:
秒;(3)存在,综上:![]() 18秒或16.8秒或12秒或
18秒或16.8秒或12秒或![]() .
.
【解析】
(1)解方程![]() 得两根为12和16,所以
得两根为12和16,所以![]() ,
,![]() ;
;
(2)设点![]() 运动
运动![]() 秒时,
秒时,![]() 平分
平分![]() ,如图,过点P作
,如图,过点P作![]() 于Q,利用角平分线定理把已知和未知线段都归结到直角
于Q,利用角平分线定理把已知和未知线段都归结到直角![]() 中,利用勾股定理构造方程,可求得
中,利用勾股定理构造方程,可求得![]() 的值;
的值;
(3)分别以AO为腰,A为顶点;AO为腰,O为顶点;AO为底构造等腰三角形,画图,通过计算可求得答案.
(1)方程![]() 可化成
可化成![]()
∴![]()
∵![]()
故![]() ,
,![]() ;
;
(2)设点![]() 运动
运动![]() 秒时,
秒时,![]() 平分
平分![]() ,
,
如图,过点P作![]() 于Q,
于Q,
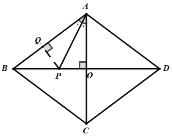
∵![]() ,
,![]() ,四边形ABCD是菱形,
,四边形ABCD是菱形,
∴![]() ,
,![]() ,
,
在直角![]() 中,∵
中,∵![]() ,
,![]() ,∴
,∴![]() ;
;
∵![]() 平分
平分![]() ,
,![]() ,
,![]() ,
,
∴![]() ,
,
![]() ,
,
![]() ,
,
![]() 为直角三角形,
为直角三角形,![]()
即:![]() ,化简并求得:
,化简并求得:![]() .
.
故答案是:![]() 秒.
秒.
(3)存在.
以![]() 为腰,
为腰,![]() 为顶点的等腰三角形,如图:
为顶点的等腰三角形,如图:
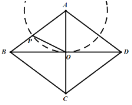
∵![]()
∴![]() ;
;
以![]() 为腰,
为腰,![]() 为顶点的等腰三角形,如图:
为顶点的等腰三角形,如图:
作![]() 于E,
于E,
在Rt![]() 和Rt
和Rt![]() 中:
中:
![]() 公共,∴Rt
公共,∴Rt![]() Rt
Rt![]()
![]() ,即
,即![]() ,∴
,∴![]() ,
,
∵![]() , ∴
, ∴![]()
∴![]() ;
;
∵![]() ,
,
∴![]() ;
;
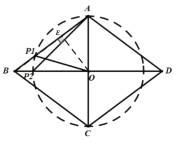
以AO为底的等腰三角形,如图:
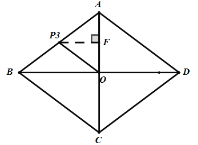
过![]() 作
作![]() 于
于![]() ,
,
![]() ,∴点F为AO中点,
,∴点F为AO中点,
![]() 四边形ABCD为菱形,∴
四边形ABCD为菱形,∴![]() ,
,
又![]() ,∴
,∴![]() ,
,
![]() 是AB中点,
是AB中点,![]() ,
,
∴![]() ;
;
综上:![]() 18秒或16.8秒或12秒或
18秒或16.8秒或12秒或![]() .
.

练习册系列答案
相关题目