Question

【题目】四边形ABCD是⊙O的内接四边形，连结AC、BD，且DA＝DB．

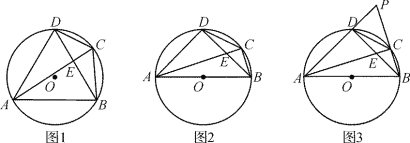
(1)如图1，∠ADB＝60°．求证：AC＝CD＋CB．

(2)如图2，∠ADB＝90°．

①求证：AC＝CD＋CB．

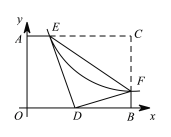
②如图3，延长AD、BC交于点P，且DC＝CB，探究线段BD与DP的数量关系，并说明理由．

Answer 1

【答案】（1）见解析；（2）①AC ＝CD ＋CB，理由见解析；②BD＝2DP，理由见解析

【解析】

（1）在AC上截取AF＝BC，连结DF，可证△DAF≌△DBC，然后证明△DFC是等边三角形，即可得到AC＝CD＋CB；

（2）在AC上截取AF＝BC，连结DF，可证△DAF≌△DBC，然后得到△DFC是等腰直角三角形，得到FC ＝DC，即可得到结论；

（3）过点D作DF⊥AC于点F，可证△CFD是等腰直角三角形，结合DC＝CB，然后得到DF=CB，可证△DFE≌△CBE，得到DE＝BE＝BD，然后证明△ADE≌△BDP，即可得到结论成立.

解：（1）如图1，证明：在AC上截取AF＝BC，连结DF．

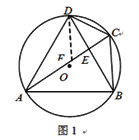
在△DAF与△DBC中，

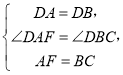
∴△DAF≌△DBC(SAS)，

∴DF＝DC，∠CDB＝∠ADF，

∵∠CDF＝∠CDB ＋∠EDF＝∠ADF ＋∠EDF＝∠ADB＝60，

∴△DFC为正三角形，

∴DC＝FC，

∴AC＝AF ＋FC＝BC ＋CD．

（2）①AC ＝CD ＋CB．

理由：如图2，在AC上截取AF＝BC，连结DF．

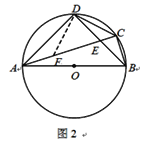
在△DAF与△DBC中，

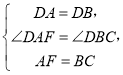
∴△DAF≌△DBC(SAS)，

∴DF＝DC，∠CDB＝∠ADF，

∵∠CDF＝∠CDB ＋∠EDF＝∠ADF ＋∠EDF＝∠ADB＝90，

∴△DFC为等腰直角三角形，

∴FC ＝DC，

∴AC＝AF ＋FC＝CD ＋CB．

②BD＝2DP．

理由：如图3，过点D作DF⊥AC于点F，

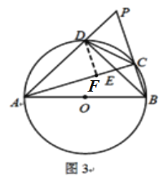
∵∠ACD＝∠ABD＝45°，

∴△CFD是等腰直角三角形，

∴CD＝DF，

∵CD＝CB，

∴DF＝CB，

在△DFE和△CBE中，

，

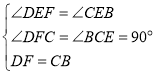∴△DFE≌△CBE(AAS)，

∴DE＝BE＝BD，

在△ADE和△BDP中，

，

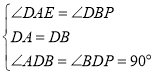∴△ADE≌△BDP(ASA)，

∴DP＝DE＝BE＝BD，

∴BD＝2DP．