ЬтФПФкШн
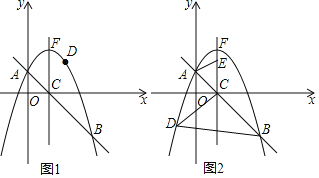
ЁОЬтФПЁПШчЭМЃЌдкЦНУцжБНЧзјБъЯЕxOyжаЃЌНЋХзЮяЯпyЃНЉx2+bx+cгыжБЯпyЃНЉx+1ЯрНЛгкЕуA(0ЃЌ1)КЭЕуB(3ЃЌЉ2)ЃЌНЛxжсгкЕуCЃЌЖЅЕуЮЊЕуFЃЌЕуDЪЧИУХзЮяЯпЩЯвЛЕуЃЎ
ЃЈ1ЃЉЧѓХзЮяЯпЕФКЏЪ§БэДяЪНЃЛ
ЃЈ2ЃЉШчЭМ1ЃЌШєЕуDдкжБЯпABЩЯЗНЕФХзЮяЯпЩЯЃЌЧѓЁїDABЕФУцЛ§зюДѓЪБЕуDЕФзјБъЃЛ
ЃЈ3ЃЉШчЭМ2ЃЌШєЕуDдкЖдГЦжсзѓВрЕФХзЮяЯпЩЯЃЌЧвЕуEЃЈ1ЃЌtЃЉЪЧЩфЯпCFЩЯвЛЕуЃЌЕБвдCЁЂBЁЂDЮЊЖЅЕуЕФШ§НЧаЮгыЁїCAEЯрЫЦЪБЃЌЧѓЫљгаТњзуЬѕМўЕФtЕФжЕЃЎ
ЁОД№АИЁПЃЈ1ЃЉyЃНЉx2+2x+1ЃЛЃЈ2ЃЉ![]() ЃЛЃЈ3ЃЉtЃН1ЛђtЃН2Лђ
ЃЛЃЈ3ЃЉtЃН1ЛђtЃН2Лђ![]() Лђ
Лђ![]()
ЁОНтЮіЁП
ЃЈ1ЃЉНЋЕуAЃЈ0ЃЌ1ЃЉКЭЕуBЃЈ3ЃЌ-2ЃЉДњШыХзЮяЮяЯпy=-x2+bx+cжаЃЌСаГіЗНГЬзщМДПЩНтД№ЃЛ
ЃЈ2ЃЉЙ§ЕуDзї DMЁЮyжсНЛABгкЕуMЃЌDЃЈaЃЌ-a2+2a+1ЃЉЃЌдђMЃЈaЃЌ-a+1ЃЉЃЌБэДяГіDMЃЌНјЖјБэДяГіЁїABDЕФУцЛ§ЃЌРћгУЖўДЮКЏЪ§ЕФаджЪЕУГізюДѓжЕМАDЕузјБъЃЛ
ЃЈ3ЃЉгЩЬтвтПЩжЊЃЌЁЯACE=ЁЯACO=45ЁуЃЌдђЁїBCDжаБигавЛИіФкНЧЮЊ45ЁуЃЌгаСНжжЧщПіЃКЂйШєЁЯCBD=45ЁуЃЌЕУГіЁїBCDЪЧЕШбќжБНЧШ§НЧаЮЃЌвђДЫЁїACEвВЪЧЕШбќжБНЧШ§НЧаЮЃЌдйЁїACEНјааЗжРрЬжiТлЃЛЂкШєЁЯCDB=45ЃЌИљРЈдВЕФаджЪШЗЖЈD1ЕФЮЛжУЃЌЧѓГіD1ЕФзјБъЃЌдйЖдЁїACEгыЁїCD1BЯрЫЦЗжРрЬжТлЃЎ
НтЃКЃЈ1ЃЉНЋЕуAЃЈ0ЃЌ1ЃЉКЭЕуBЃЈ3ЃЌЉ2ЃЉДњШыХзЮяЮяЯпyЃНЉx2+bx+cжа
ЕУ![]() ЃЌ
ЃЌ
НтЕУ![]()
ЁрyЃНЉx2+2x+1ЃЛ
ЃЈ2ЃЉШчЭМ1ЫљЪОЃКЙ§ЕуDзї DMЁЮyжсНЛABгкЕуMЃЌ
ЩшDЃЈaЃЌЉa2+2a+1ЃЉЃЌдђMЃЈaЃЌЉa+1ЃЉ
ЃЎЁрDMЃНЉa2+2a+1ЉЃЈЉa+1ЃЉЃНЉa2+3a
Ёр![]()
Ёп![]()
![]() ЃЌ
ЃЌ![]() газюДѓжЕЃЌ
газюДѓжЕЃЌ
ЕБ![]() ЪБЃЌ
ЪБЃЌ![]()
ДЫЪБ![]()

ЭМ1
ЃЈ3ЃЉЁпOAЃНOCЃЌШчЭМ2ЃЌCFЁЮyжсЃЌ
ЁрЁЯACEЃНЁЯACOЃН45ЁуЃЌ
ЁрЁїBCDжаБигавЛИіФкНЧЮЊ45ЁуЃЌгЩЬтвтПЩжЊЃЌЁЯBCDВЛПЩФмЮЊ45ЁуЃЌ
ЂйШєЁЯCBDЃН45ЁуЃЌдђBDЁЮxжсЃЌ
ЁрЕуDгыЕуBгкХзЮяЯпЕФГЦжсжБЯпxЃН1ГЦЃЌЩшBDгыжБЯпЃН1НЛгкЕуHЃЌдђHЃЈ1ЃЌЉ2ЃЉ
BЃЈ3ЃЌЉ2ЃЉЃЌDЃЈЉ1ЃЌЉ2ЃЉ
ДЫЪБЁїBCDЪЧЕШбќжБНЧШ§НЧаЮЃЌвђДЫЁїACEвВЪЧЕШбќжБНЧШ§НЧаЮЃЌ
ЃЈiЃЉЕБЁЯAECЃН90ЁуЪБЃЌЕУЕНAEЃНCEЃН1ЃЌ
ЁрEЃЈ1.1ЃЉЃЌЕУЕНtЃН
ЃЈiiЃЉЕБЁЯCAEЃН90ЪБЃЌЕУЕНЃКACЃНAEЃН![]() ЃЌ
ЃЌ
ЁрCEЃН2ЃЌЁрEЃЈ1.2ЃЉЃЌЕУЕНtЃН2
ЭМ2
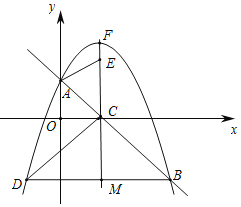
ЂкШєЁЯCDBЃН45ЁуЃЌШчЭМ3ЃЌЂйжаЕФЧщПіЪЧЦфжавЛжжЃЌД№АИЭЌЩЯ
вдЕуHЮЊдВаФЃЌHBЮЊАыОЖзїдВЃЌдђЕуBЁЂCЁЂDЖМдкдВHЩЯЃЌ
ЩшдВHгыЖдГЦзѓВрЕФЮяЯпНЛгкСэвЛЕуD1ЃЌ
дђЁЯCD1BЃНЁЯCDBЃН45ЁуЃЈЭЌЛЁЫљЖдЕФдВжмНЧЯрЕШЃЉЃЌМДD1вВЗћКЯЬтвт
Щш![]()
гЩHD1ЃНDHЃН2
НтЕУn1ЃНЉ1ЃЈКЌШЅЃЉЃЌn2ЃН3ЃЈЩсШЅЃЉЃЌ![]() ЃЈЩсШЅЃЉЃЌ
ЃЈЩсШЅЃЉЃЌ![]()
Ёр![]() ЃЌ
ЃЌ
дђ![]() ЃЌ
ЃЌ
![]()
ЃЈiЃЉШєЁїACEЁзЁїCD1BЃЌ
дђ![]() ЃЌ
ЃЌ
МД ЃЌ
ЃЌ
НтЕУ![]() ЃЌ
ЃЌ![]() ЃЈЩсШЅЃЉ
ЃЈЩсШЅЃЉ
ЃЈiiЃЉЁїACEЁзЁїBD1Cдђ![]() ЃЌ
ЃЌ
МД ЃЌ
ЃЌ
НтЕУ![]() ЃЌ
ЃЌ![]() ЃЈЩсШЅЃЉ
ЃЈЩсШЅЃЉ
злЩЯЫљЪіЃКЫљгаТњзуЬѕМўЕФtЕФжЕЮЊtЃН1ЛђtЃН2Лђ![]() Лђ
Лђ![]()

ЭМ3

 ЧсЫЩЖсЙкШЋФмеЦПиОэЯЕСаД№АИ
ЧсЫЩЖсЙкШЋФмеЦПиОэЯЕСаД№АИ