题目内容
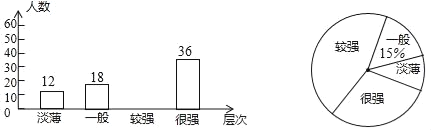
【题目】2020年春节前夕“新型冠状病毒”爆发,国家教育部要求各地延期开学,并要求:利用网络平台,“停课不停学”.为响应号召,某校师生根据上级要求积极开展网络授课教学,八年级为了解学生网课发言情况,随机抽取该年级部分学生,对他们某天在网课上发言的次数进行了统计,其结果如下表,并绘制了如图所示的两幅不完整的统计图,已知B、E两组发言人数的比为5:2,请结合图中相关数据回答下列问题:
(1)求出样本容量,并补全直方图,在扇形统计图中,“B”所对应的圆心角的度数是 ;
(2)该年级共有学生500人,估计全年级在这天里发言次数不少于12的人数为 ;
(3)该校八年级组织一次网络授课经验专项视频会议,A组的中恰有1位女生,E组的中有位2男生.现从A组与E组中分别抽一位写报告,利用“树状图”或列表法求出正好选中一男一女的概率.
n | |
A |
|
B |
|
C |
|
D |
|
E |
|
F |
|

【答案】(1)图见解析,72°;(2)90人;(3)![]() .
.
【解析】
(1)由B、E两组发言人数的比为5:2,B组人数为10人得出E组人数为4人,再结合E组对应百分比可得样本容量,继而利用分组人数=总人数×对应百分比求解可得;
(2)用总人数乘以E、F组人数和所占比例即可得;
(3)分别求出A、E两组的人数,确定出各组的男女生人数,然后列表或画树状图,再根据概率公式计算即可得解.
解:(1)∵B、E两组发言人数的比为5:2,B组人数为10人,
∴E组人数为4人,
则样本容量为4÷8%=50,
A组人数为50×6%=3(人),C组人数为50×30%=15(人),D组人数为50×26%=13(人),F组人数为50-(3+10+15+13+4)=5(人),
补全直方图如下: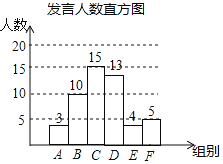
在扇形统计图中,“B”所对应的圆心角的度数是360°×![]() =72°,
=72°,
(2)估计全年级在这天里发言次数不少于12的人数为500×![]() =90(人);
=90(人);
(3)A组发言的学生:50×6%=3人,所以有1位女生,2位男生,
E组发言的学生:50×8%=4人,所以有2位女生,2位男生,
列表如下: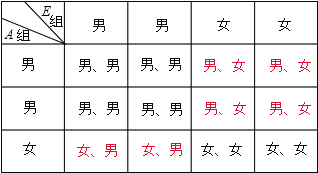
画树状图如下: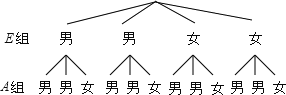
共12种情况,其中一男一女的情况有6种,
所以P(一男一女)=![]() .
.

【题目】为弘扬传统文化,某校开展了“传承经典文化,阅读经典名著”活动.为了解七、八年级学生(七、八年级各有600名学生)的阅读效果,该校举行了经典文化知识竞赛.现从两个年级各随机抽取20名学生的竞赛成绩(百分制)进行分析,过程如下:
收集数据:
七年级:79,85,73,80,75,76,87,70,75,94,75,79,81,71,75,80,86,59,83,77.
八年级:92,74,87,82,72,81,94,83,77,83,80,81,71,81,72,77,82,80,70,41.
整理数据:
|
|
|
|
|
| |
七年级 | 0 | 1 | 0 | a | 7 | 1 |
八年级 | 1 | 0 | 0 | 7 | b | 2 |
分析数据:
平均数 | 众数 | 中位数 | |
七年级 | 78 | 75 |
|
八年级 | 78 |
| 80.5 |
应用数据:
(1)由上表填空:a= ,b= ,c= ,d= .
(2)估计该校七、八两个年级学生在本次竞赛中成绩在90分以上的共有多少人?
(3)你认为哪个年级的学生对经典文化知识掌握的总体水平较好,请说明理由.