题目内容
【题目】对角线长分别为![]() 和
和![]() 的菱形
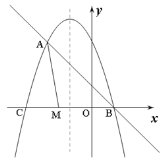
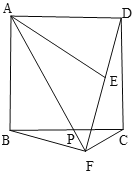
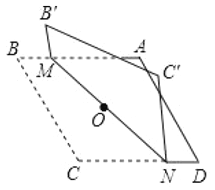
的菱形![]() 如图所示,点
如图所示,点![]() 为对角线的交点.过点
为对角线的交点.过点![]() 折叠菱形,使
折叠菱形,使![]() 两点重合,
两点重合,![]() 是折痕,若
是折痕,若![]() ,则
,则![]() 的长为( )
的长为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
【答案】A
【解析】
连接AC、BD,利用菱形的性质得OC=![]() AC=3,OD=
AC=3,OD=![]() BD=4,∠COD=90°,再利用勾股定理计算出CD=5,由ASA证得△OBM≌△ODN得到DN=BM,然后根据折叠的性质得BM=B'M=1.5,则DN=1.5,即可得出结果.
BD=4,∠COD=90°,再利用勾股定理计算出CD=5,由ASA证得△OBM≌△ODN得到DN=BM,然后根据折叠的性质得BM=B'M=1.5,则DN=1.5,即可得出结果.
解:连接AC、BD,如图,
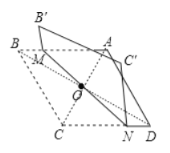
∵点O为菱形ABCD的对角线的交点,
∴OC=![]() AC=3,OB=OD=
AC=3,OB=OD=![]() BD=4,∠COD=90°,
BD=4,∠COD=90°,
在Rt△COD中,根据勾股定理,得CD=5,
∵AB∥CD,
∴∠MBO=∠NDO,
在△OBM和△ODN中,∠MBO=∠NDO,OB=OD,∠BOM=∠DON,∴△OBM≌△ODN(ASA),
∴DN=BM,
∵过点O折叠菱形,使B,B′两点重合,MN是折痕,
∴BM=B'M=1.5,
∴DN=1.5,
∴CN=CD-DN=5-1.5=3.5,
故选:A.

练习册系列答案
相关题目