题目内容
【题目】在平面直角坐标系中,矩形OABC的顶点O、A、C的坐标分别为O(0,0),A(﹣x,0),C(0,y),且x、y满足![]() .
.
(1)矩形的顶点B的坐标是 .
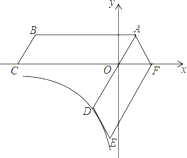
(2)若D是AB中点,沿DO折叠矩形OABC,使A点落在点E处,折痕为DO,连BE并延长BE交y轴于Q点.
①求证:四边形DBOQ是平行四边形.
②求△OEQ面积.
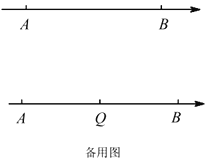
(3)如图2,在(2)的条件下,若R在线段AB上,AR=4,P是AB左侧一动点,且∠RPA=135°,求QP的最大值是多少?

【答案】(1)点B(﹣4,6);(2)①见解析;②S△EOQ=![]() ;(3)PQ的最大值为2
;(3)PQ的最大值为2![]() +
+![]()
【解析】
(1)由题意可求x=4,y=6,即可求点B坐标;
(2)①由折叠性质可得AD=DE,∠ADO=∠ODE,由三角形外角性质可得∠ADO=∠DBE,可得OD∥BQ,即可证四边形BDOQ是平行四边形;②由题意可证△BFD∽△QCB,可得![]() ,可求
,可求![]() ,,由S△EOQ=SBDOQ-S△DEO-S△BDE可得△OEQ面积;
,,由S△EOQ=SBDOQ-S△DEO-S△BDE可得△OEQ面积;
(3)连接RO,以RO为直径作圆H,作HF⊥OQ于点F,由题意可得点A,点P,点R,点O四点共圆,即点P在以点H为圆心,RO为直径的圆上,则点P,点H,点Q三点共线时,PQ值最大,由勾股定理可求![]() ,即可求QP的最大值.
,即可求QP的最大值.
解:(1)∵x﹣4≥0,4﹣x≥0
∴x=4,
∴y=6
∴点A(﹣4,0),点C(0,6)
∴点B(﹣4,6)
故答案为(﹣4,6)
(2)①∵D是AB中点,
∴AD=BD
∵折叠
∴AD=DE,∠ADO=∠ODE
∴∠DBE=∠DEB
∵∠ADE=∠DBE+∠DEB
∴∠ADO+∠ODE=∠DBE+∠DEB
∴∠ADO=∠DBE
∴OD∥BQ,且AB∥OC
∴四边形BDOQ是平行四边形,
②如图,过点D作DF⊥BQ于点F,

∵AD=3,AO=4
∴DO=![]() =5
=5
∵四边形BDOQ是平行四边形,
∴BD=OQ=3,BQ=DO=5,
∴CQ=CO﹣OQ=3
∵AB∥CO
∴∠ABQ=∠BQC,且∠BFD=∠BCQ=90°
∴△BFD∽△QCB
∴![]()
![]()
![]()
∵DE=BD,DF⊥BQ
![]()
![]() ,
,
∴SBDOQ=12
∴S△EOQ=SBDOQ﹣S△DEO﹣S△BDE=![]()
(3)如图,连接RO,以RO为直径作圆H,作HF⊥OQ于点F,

∵RA=4=AO
∴∠AOR=∠ARO=45°,RO=![]()
∵∠APR+∠AOR=135°+45°=180°
∴点A,点P,点R,点O四点共圆
∴点P在以点H为圆心,RO为直径的圆上,
∴点P,点H,点Q三点共线时,PQ值最大,
∵∠HOF=45°,HF⊥OQ,
∴∠FHO=∠HOF=45°,且OH=![]()
∴HF=OF=2,
∴QF=OQ﹣OF=3﹣2=1
∴HQ=![]()
∴PQ的最大值为![]() .
.

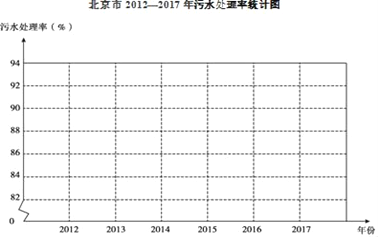
【题目】北京市积极开展城市环境建设,其中污水治理是重点工作之一,以下是北京市2012﹣2017年污水处理率统计表:
年份 | 2012 | 2013 | 2014 | 2015 | 2016 | 2017 |
污水处理率(%) | 83.0 | 84.6 | 86.1 | 87.9 | 90.0 | 92.0 |
(1)用折线图将2012﹣2017年北京市污水处理率表示出来,并在图中标明相应的数据;
(2)根据统计图表中提供的信息,预估2018年北京市污水处理率约为_____%,说明你的预估理由:_____.