题目内容
【题目】已知:![]() 中,
中,![]() ,
,![]() ,点
,点![]() 为
为![]() 内一点,连接
内一点,连接![]() ,
,![]() ,
,![]() ,过点
,过点![]() 作
作![]() ,交
,交![]() 的延长线于点
的延长线于点![]() .
.


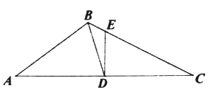
(1)如图1,求证:![]() ;
;
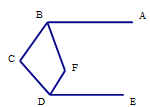
(2)如图2,点![]() 为
为![]() 的中点,分别连接
的中点,分别连接![]() ,
,![]() ,求
,求![]() 的度数;
的度数;
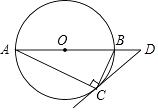
(3)如图3,在(2)的条件下,点![]() 为
为![]() 上一点,连接
上一点,连接![]() ,点
,点![]() 为
为![]() 的中点,连接
的中点,连接![]() ,过点
,过点![]() 作
作![]() ,交
,交![]() 的延长线于点
的延长线于点![]() ,若
,若![]() ,
,![]() 的面积为30,
的面积为30,![]() ,求线段
,求线段![]() 的长.
的长.
【答案】(1)见解析;(2)45°;(3)10![]()
【解析】
(1)根据全等三角形的判定得出△CAE≌△ABD,进而利用全等三角形的性质得出AE=BD;
(2)根据全等三角形的判定得出△AEH≌△BDH,进而利用全等三角形的性质解答;
(3)过点M作MS⊥FH于点S,过点E作ER⊥FH,交HF的延长线于点R,过点E作ET∥BC,根据全等三角形判定和性质解答即可.
证明:(1)∵CE⊥AE,BD⊥AE,
∴∠AEC=∠ADB=90°,
∵∠BAC=90°,
∴∠ACE+CAE=∠CAE+∠BAD=90°,
∴∠ACE=∠BAD,
在△CAE与△ABD中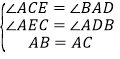
∴△CAE≌△ABD(AAS),
∴AE=BD;
(2)连接AH,如图2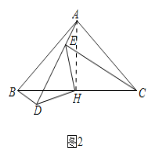
∵AB=AC,BH=CH,![]() ,
,
∴∠BAH=![]() ∠BAC=
∠BAC=![]() ×90°=45°,∠AHB=90°,
×90°=45°,∠AHB=90°,
∴∠ABH=∠BAH=45°,
∴AH=BH,
∵∠EAH=∠BAH-∠BAD=45°-∠BAD,
∠DBH=180°-∠ADB-∠BAD-∠ABH=45°-∠BAD,
∴∠EAH=∠DBH,
在△AEH与△BDH中 ∴△AEH≌△BDH(SAS),
∴△AEH≌△BDH(SAS),
∴EH=DH,∠AHE=∠BHD,
∴∠AHE+∠EHB=∠BHD+∠EHB=90°
即∠EHD=90°,
∴∠EDH=∠DEH=![]() =45°
=45°
(3)过点M作MS⊥FH于点S,过点E作ER⊥FH,交HF的延长线于点R,过点E作ET∥BC,交HR的延长线于点T.如图3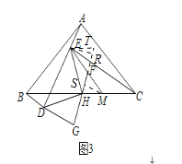
∵DG⊥FH,ER⊥FH,
∴∠DGH=∠ERH=90°,
∴∠HDG+∠DHG=90°
∵∠DHE=90°,
∴∠EHR+∠DHG=90°,
∴∠HDG=∠HER
在△DHG与△HER中
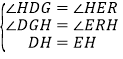 ∴△DHG≌△HER(AAS),
∴△DHG≌△HER(AAS),
∴HG=ER,
∵ET∥BC,
∴∠ETF=∠BHG,∠EHB=∠HET,
∴∠ETF=∠FHM,
∵∠EHB=∠BHG,
∴∠HET=∠ETF,
∴HE=HT,
在△EFT与△MFH中
 ,
,
∴△EFT≌△MFH(AAS),
∴HF=FT,
∵![]() =
=![]() ,
,
∴ER=MS,
∴HG=ER=MS,
设GH=6k,FH=5k,则HG=ER=MS=6k,
∴![]() ==30,
==30,
∴k=![]() ,
,
∴FH=5![]() ,
,
∴HE=HT=2HF=10![]() ,
,