题目内容
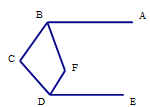
【题目】如图,已知![]() //
//![]() ,
,![]()
![]()
![]() ,∠
,∠![]() 和∠
和∠![]() 的角平分线交于点F,∠
的角平分线交于点F,∠![]() =__________°.
=__________°.
【答案】135;
【解析】
连接BD,根据三角形内角和定理得出∠C+∠CBD+∠CDB=180°,再由BC⊥CD可知∠C=90°,故∠CBD+∠CDB=90°,再由AB∥DE可知∠ABD+∠BDE=180°,故∠CBD+∠CDB+∠ABD+∠BDE =270°,再由∠ABC和∠CDE的平分线交于点F可得出∠CBF+∠CDF的度数,由四边形内角和定理即可得出结论.
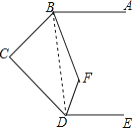
解:连接BD,
∵∠C+∠CBD+∠CDB=180°,BC⊥CD,
∴∠C=90°,
∴∠CBD+∠CDB=90°.
∵AB∥DE,
∴∠ABD+∠BDE=180°,
∴∠CBD+∠CDB+∠ABD+∠BDE=90°+180°=270°,即∠ABC+∠CDE=270°.
∵∠ABC和∠CDE的平分线交于点F,
∴∠CBF+∠CDF=![]() ×270°=135°,
×270°=135°,
∴∠BFD=360°-90°-135°=135°.
故答案为:135.

练习册系列答案
 暑假作业暑假快乐练西安出版社系列答案
暑假作业暑假快乐练西安出版社系列答案
相关题目