题目内容
【题目】在等边
所在平面内有点P，且使得
，
，
均为等腰三角形，则符合条件的点P共有______个
【答案】10
【解析】
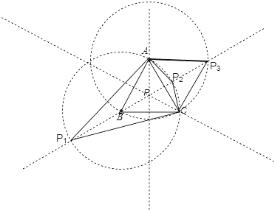
过B点作
的中垂线，可知在三角形内有一点P满足
、
、
都是等腰三角形，根据等腰三角形的性质可以做两个圆，圆B和圆A，从而可以得出一条中垂线上有四个点满足、、都是等腰三角形，而三角形内部的一点是重合的，所以可以得出共有10个点．
解：作三边的中垂线，交点P肯定是其中之一，以B为圆心，BA为半径画圆，交AC的中垂线于
、
两点，作
、
、
，它们也都是等腰三角形，因此、是具有题目所说的性质的点；
以A为圆心，BA为半径画圆，交AC的中垂线于点
、也必具有题目所说的性质．
依此类推，在的其余两条中垂线上也存在这样性质的点，所以这些点一共有：
个．
故答案为10．
练习册系列答案
名校课堂系列答案
相关题目
