题目内容
【题目】如图,已知点O为两内角平分线交点,∠A= 80°,则∠BOC=_______ 。
【答案】130度
【解析】(1)先根据三角形内角和定理求出∠ABC+∠ACB的度数,再根据BO、CO分别平分∠ABC与∠ACB求出∠1+∠2的度数,由三角形内角和定理即可得出∠BOC的度数;
解:如图所示,
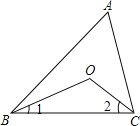
∵∠A=80°,
∴∠ABC+∠ACB=180°-80°=100°.
∵BO、CO分别是∠ABC、∠ACB的角平分线,
∴∠1+∠2=![]() (∠ABC+∠ACB)=
(∠ABC+∠ACB)=![]() ×100°=50°,
×100°=50°,
∴∠BOC=180°-(∠1+∠2)=180°-50°=130°.
“点睛”本题考查的是三角形内角和定理以及角平分线的性质,熟知三角形内角和是180°是解答此题的关键.求角的度数常常要用到“三角形的内角和是180°”这一隐含的条件以及三角形的外角通常情况下是转化为内角来解决.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目