Question

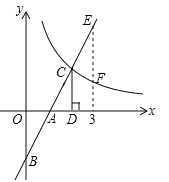
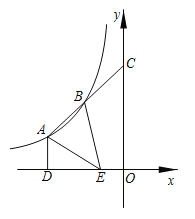
【题目】如图，A，B是反比例函数(k≠0)图象上的两点，延长线段AB交y轴于点C，且B为线段AC的中点，过点A作AD⊥x轴于点D，E为线段OD的三等分点，且OE＜DE．连接AE，BE．若S△ABE＝7，则k的值为_________．

Answer 1

【答案】-12

【解析】

设A（m，），C（0，n），则D（m，0），E（m，0），由AB＝BC，推出B（，），根据点B在上，求出mn＝3k，连接EC，OA，因为AB＝BC，推出S△AEC＝2S△AEB＝14，根据S△AEC＝S△AEO＋S△ACO－S△ECO，构建方程即可解决问题；

解：设A(m，)，C(0，n)，则D(m，0)，E(m，0)，

∵B为AC的中点，

∴AB＝BC，

∴B(，)，

∵点B在反比例函数 (k≠0)的图象上，

∴

∴k＋mn＝4k，

∴mn＝3k，

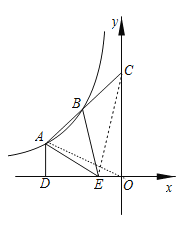
如图，连接EC，OA，

∵AB＝BC，

∴S△AEC＝2S△AEB＝14，

∵S△AEC＝S△AEO＋S△ACO－S△ECO，

∴14＝，

∴14＝，

∴k＝－12．