题目内容
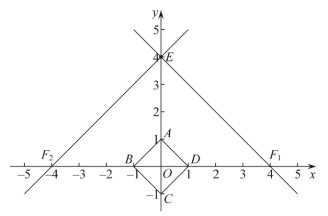
【题目】在平面直角坐标系![]() 中,正方形ABCD的顶点分别为A(0,1),B(-1,0),C(0,-1),D(1,0).对于图形M,给出如下定义:P为图形M上任意一点,Q为正方形ABCD边上任意一点,如果P,Q两点间的距离有最大值,那么称这个最大值为图形M的“正方距”,记作
中,正方形ABCD的顶点分别为A(0,1),B(-1,0),C(0,-1),D(1,0).对于图形M,给出如下定义:P为图形M上任意一点,Q为正方形ABCD边上任意一点,如果P,Q两点间的距离有最大值,那么称这个最大值为图形M的“正方距”,记作![]() .
.
(1)已知点![]() ,
,
①直接写出![]() 的值;
的值;
②直线![]() 与x轴交于点F,当
与x轴交于点F,当![]() 取最小值时,求k的取值范围;
取最小值时,求k的取值范围;
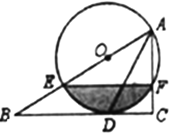
(2)![]() 的圆心为
的圆心为![]() ,半径为1.若
,半径为1.若![]() ,直接写出t的取值范围.
,直接写出t的取值范围.
【答案】(1)①5.②见解析;(2)![]() .
.
【解析】
(1) ①根据题意![]() 是指点
是指点![]() 到正方形
到正方形![]() 上动点
上动点![]() 的最大距离,所以当点
的最大距离,所以当点![]() 与点
与点![]() 重合时,此时
重合时,此时![]() 最大为
最大为![]() ;
;
②根据![]() 的最小值是,可知
的最小值是,可知![]() ,所以当直线
,所以当直线![]() 经过
经过![]() 和
和![]() ,即可求出
,即可求出![]() 的值;
的值;
(2)根据圆心![]() ,半径为
,半径为![]() ,可知圆
,可知圆![]() 在直线
在直线![]() 的直线上动,因为
的直线上动,因为![]() 圆上动点
圆上动点![]() 到正方形边上动点
到正方形边上动点![]() 的最大值,所以可以转化成
的最大值,所以可以转化成 ![]() 圆的半径
圆的半径![]() 圆心
圆心![]() 到正方形边上动点
到正方形边上动点![]() ,因为
,因为![]() ,可以算出
,可以算出![]() 的分界点,由于圆心
的分界点,由于圆心![]() 到点Q的最大值存在一种情况
到点Q的最大值存在一种情况![]() 时,可以计算出
时,可以计算出![]() ,刚好
,刚好![]() ,即可求出符合题意
,即可求出符合题意![]() 的取值范围.
的取值范围.
解:1.①由根据题意![]() 是指点
是指点![]() 到正方形
到正方形![]() 上动点
上动点![]() 的最大距离,所以当点
的最大距离,所以当点![]() 与点
与点![]() 重合时,此时
重合时,此时![]() 最大,即
最大,即![]()
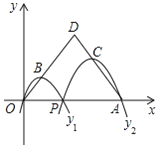
②如图所示:
∵![]() .
.
当点![]() 的横坐标在
的横坐标在![]() 时,
时,![]() ,
,
当点![]() 的横坐标在
的横坐标在![]() 时,
时,![]() ,
,
∵![]() 要取最小值,
要取最小值,
∴![]()
∴符合题意的点F满足![]()
∴当直线![]() 经过点
经过点![]() 的坐标为
的坐标为![]() 和点
和点![]() 的坐标为
的坐标为![]() 是分别求得
是分别求得![]() .
.
∴![]() 或
或![]() .
.
结合函数图象可得![]() 或
或![]() .
.
(2)由题意可知:![]()
![]()
![]() 时
时
![]() 可计算当
可计算当![]() 时,
时,
当圆心![]() 在
在![]() 轴左侧时
轴左侧时
![]() 可以考虑到当
可以考虑到当![]() 时,
时,
利用两点之间的距离公式:
即![]()
求得:![]() ,
,
![]()
![]() 当
当![]() 时,
时,![]() ,即
,即![]()
当圆心![]() 在
在![]() 轴右侧时
轴右侧时
![]() 可以考虑到当
可以考虑到当![]() 时,
时,
利用两点之间的距离公式:
即![]()
求得:![]() ,
,
![]()
![]() 当
当![]() 时,
时,![]() ,即
,即![]()
![]()
![]()
![]()
![]()

练习册系列答案
 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案
相关题目