题目内容
【题目】某市制药厂需要紧急生产一批药品,要求必须在12天(含12天)内完成.为了加快生产,车间采取工人加班,机器不停的生产方式,这样每天药品的产量y(吨)是时间x(天)一次函数,且满足表中所对应的数量关系.由于机器负荷运转产生损耗,平均生产每吨药品的成本P(元)与时间x(天)的关系满足图中的函数图象. 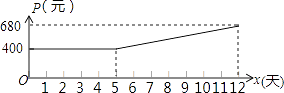
时间x(天) | 2 | 4 |
每天产量y(吨) | 24 | 28 |
(1)求药品每天的产量y(吨)是时间x(天)之间的函数关系式;
(2)当5≤x≤12时,直接写出P(元)与时间x(天)的函数关系是P=;
(3)若这批药品的价格为1400元/吨,每天的利润设为W元,求哪一天的利润最高,最高利润是多少?(利润=价格﹣成本)
(4)为了提高工人加班的津贴,药厂决定在(3)中价格的基础上每吨药品加价a元,但必须满足从第5天到第12天期间,每吨加价a后每天的利润随时间的增大而增大,直线写出a的最小值.
【答案】
(1)解:设y=kx+b,则 ![]() 解得
解得 ![]() ,
,
∴y=2x+20
(2)P=40x+200
(3)解:当1≤x≤5时,平均生产每吨药品的成本是P=400元,
此时利润W1=(1400﹣400)y=1000(2x+20)=2000x+20000,
∵2000>0,
∴W1随x增大而增大,
∴x=5时,W1最大值=2000×5+20000=30000元.
当6≤x≤12时,平均生产每吨药品的成本是P=40x+200,
此时利润W2=(1400﹣P)y=(1400﹣40x﹣200)(2x+20)=﹣80x2+1600x+24000=﹣80(x﹣10)2+32000,
∴x=10时,W2最大值=32000,
∵32000>3000,
∴第10天利润最高,最高利润是32000元
(4)解:a的最小值为160.,
∵5≤x≤12,
∴Q=(1400+a﹣40x﹣200)(2X+20)=﹣80x2+(1600+2a)x+(24000+20a),
∵﹣80<0,
∴抛物线开口向下,在对称轴左侧,Q随x增大而增大,
∴﹣ ![]() ≥12,
≥12,
解得a≥160,
∴a的最小值为160
【解析】解:(2)设P=k′x+b′,则 ![]() ,解得
,解得 ![]() ,
,
∴P=40x+200.
所以答案是P=40x+200.

【题目】探究题.
用棋子摆成的“T”字形图如图所示:

(1)填写表:
图形序号 | ① | ② | ③ | ④ | … | ⑩ |
每个图案中棋子个数 | 5 | 8 | … |
(2)写出第n个“T”字形图案中棋子的个数(用含n的代数式表示);
(3)第20个“T”字形图案共有棋子多少个?
(4)计算前20个“T”字形图案中棋子的总个数.(提示:请你先思考下列问题:第1个图案与第20个图案中共有多少个棋子?第2个图案与第19个图案中共有多少个棋子?第3个图案与第18个图案呢?)