��Ŀ����
����Ŀ��̽���⣮
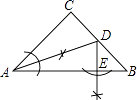
�����Ӱڳɵ���T������ͼ��ͼ��ʾ��

��1�������
ͼ����� | �� | �� | �� | �� | �� | �� |
ÿ��ͼ�������Ӹ��� | 5 | 8 | �� |
��2��д����n����T������ͼ�������ӵĸ������ú�n�Ĵ���ʽ��ʾ����
��3����20����T������ͼ���������Ӷ��ٸ���
��4������ǰ20����T������ͼ�������ӵ��ܸ���������ʾ��������˼���������⣺��1��ͼ�����20��ͼ���й��ж��ٸ����ӣ���2��ͼ�����19��ͼ���й��ж��ٸ����ӣ���3��ͼ�����18��ͼ���أ���
���𰸡���1������������2��3n+2�����ӣ���3��62������4��670����
�����������������
��1���۲�������ͼ�οɵã���ȥ��1��ͼ���⣬�����ÿ1��ͼ����ǰ��1��ͼ����ȣ����Ŷ���2�����ӣ����ж���1����������ÿһ��ͼ�������ӵ���������һ��ͼ�������ӵ�������3���ɴ˿ɵõ�n��ͼ���У����ӵĸ���Ϊ5+3��n��1�����������ɽ�ã�1������3��С��Ĵ𰸣�
��2����ڣ�4��С��ʱ������Ŀ�е���ʾ�����֪����1��ͼ�κ͵�20��ͼ���й���67�����ӣ���2��ͼ�κ͵�19��ͼ���й���67�ţ��������ɴ˼��ɵã�ǰ20��ͼ������������Ϊ��67��10=670��.
���������
�۲�������ͼ�οɵã�
�ڳɵ�1����T������Ҫ5�����ӣ�
�ڳɵ�2����T������Ҫ8�����ӣ�8��5=3��
�ڳɵ�3����T������Ҫ11�����ӣ�11��8=3��
�ڳɵ�4����T������Ҫ14�����ӣ�14��11=3��
��
�ڳɵ�10����T������Ҫ32�����ӣ�
��
�ɴ˿ɵó����ɣ��ڳɵ�n����T������Ҫ5+3��n��1��=3n+2�����ӣ�
��1�������������ɼ�����д������ȱ����Ϊ��
ͼ����� | �� | �� | �� | �� | �� | �� |
ÿ��ͼ�������Ӹ��� | 5 | 8 | 11 | 14 | �� | 32 |
��2����n����T������ͼ�������ӵĸ���Ϊ��5+3��n��1��=(3n+2)�����ӣ�
��3�����ݵ�n����T������ͼ�������ӵĸ���Ϊ3n+2����ɵã�
��18����T������Ҫ56�����ӣ���19����T������Ҫ59����������20����T������Ҫ62�����ӣ�
��4����1��ͼ�����20��ͼ��������5+62=67�����ӣ�
��2��ͼ�����19��ͼ��������8+59=67�����ӣ�
��3��ͼ�����18��ͼ��������11+56=67��������
������
�ɴ˿�֪��ǰ20����T������ͼ�������ӵ��ܸ���Ϊ��67��10=670��������

����Ŀ��ij����ҩ����Ҫ��������һ��ҩƷ��Ҫ�������12�죨��12�죩����ɣ�Ϊ�˼ӿ������������ȡ���˼Ӱ࣬������ͣ��������ʽ������ÿ��ҩƷ�IJ���y���֣���ʱ��x���죩һ�κ������������������Ӧ��������ϵ�����ڻ���������ת������ģ�ƽ������ÿ��ҩƷ�ijɱ�P��Ԫ����ʱ��x���죩�Ĺ�ϵ����ͼ�еĺ���ͼ�� 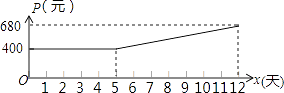
ʱ��x���죩 | 2 | 4 |
ÿ�����y���֣� | 24 | 28 |
��1����ҩƷÿ��IJ���y���֣���ʱ��x���죩֮��ĺ�����ϵʽ��
��2����5��x��12ʱ��ֱ��д��P��Ԫ����ʱ��x���죩�ĺ�����ϵ��P=��
��3��������ҩƷ�ļ۸�Ϊ1400Ԫ/�֣�ÿ���������ΪWԪ������һ���������ߣ���������Ƕ��٣�������=�۸ɱ���
��4��Ϊ����߹��˼Ӱ�Ľ�����ҩ�������ڣ�3���м۸�Ļ�����ÿ��ҩƷ�Ӽ�aԪ������������ӵ�5�쵽��12���ڼ䣬ÿ�ּӼ�a��ÿ���������ʱ������������ֱ��д��a����Сֵ��