题目内容
【题目】连接正八边形的三个顶点,得到如图所示的图形,下列说法错误的是( ) 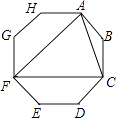
A.△ACF是等边三角形
B.连接BF,则BF分别平分∠AFC和∠ABC
C.整个图形是轴对称图形,但不是中心对称图形
D.四边形AFGH与四边形CFED的面积相等
【答案】A
【解析】解:∵八边形ABCDEFGH是正八边形,
∴AB=CB=AH=GH=GF=EF=DE=CD,AF=CF,∠AFC=90°﹣45°=45°,
∴∠FAC=∠FCA=(180°﹣45°)=67.5°,
∴△ACF不是等边三角形,选项A错误;
∵正八边形是轴对称图形,直线BF是对称轴,
∴连接BF,则BF分别平分∠AFC和∠ABC,
∴选项B、C正确;
∵四边形AFGH与四边形CFED的面积相等,
∴选项D正确;
故选:A.
【考点精析】利用正多边形和圆和轴对称图形对题目进行判断即可得到答案,需要熟知圆的内接四边形的对角互补,并且任何一个外角都等于它的内对角;圆的外切四边形的两组对边的和相等;两个完全一样的图形关于某条直线对折,如果两边能够完全重合,我们就说这两个图形成轴对称,这条直线就对称轴.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案【题目】某市制药厂需要紧急生产一批药品,要求必须在12天(含12天)内完成.为了加快生产,车间采取工人加班,机器不停的生产方式,这样每天药品的产量y(吨)是时间x(天)一次函数,且满足表中所对应的数量关系.由于机器负荷运转产生损耗,平均生产每吨药品的成本P(元)与时间x(天)的关系满足图中的函数图象. 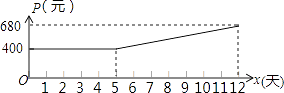
时间x(天) | 2 | 4 |
每天产量y(吨) | 24 | 28 |
(1)求药品每天的产量y(吨)是时间x(天)之间的函数关系式;
(2)当5≤x≤12时,直接写出P(元)与时间x(天)的函数关系是P=;
(3)若这批药品的价格为1400元/吨,每天的利润设为W元,求哪一天的利润最高,最高利润是多少?(利润=价格﹣成本)
(4)为了提高工人加班的津贴,药厂决定在(3)中价格的基础上每吨药品加价a元,但必须满足从第5天到第12天期间,每吨加价a后每天的利润随时间的增大而增大,直线写出a的最小值.
【题目】用描点法画二次函数y=ax2+bx+c(a≠0)的图象时,列出了如下表格:
x | … | -1 | 0 | 1 | 2 | 3 | 4 | … |
y=ax2+bx+c(a≠0) | … | 8 | 3 | 0 | -1 | 0 | 3 | … |
那么当该二次函数值y > 0时,x的取值范围是_________.