题目内容
【题目】“体育嘉年华”活动中，学校六个班级学生在一个长方形场地上列队训练，每个班之间间隔2米，如图所示，长方形场地长为b米，宽为a米．
（1）请直接写出六个班级所占场地面积的和是多少平方米？（用a、b表示）
（2）若a=20，且班级之间间隔地带（图中阴影部分）所占面积为整个长方形场地面积的
请求出该长方形场地的长b为多少米？
【答案】(1) S= ab-4a-2b+8平方米 (2)该长方形场地的长b为36米
【解析】试题分析：（1）分别表示出平移阴影部分后矩形的长和宽即可表示出其面积；
（2）根据题意列出方程18（b﹣2）=
×20×b求解即可．
试题解析：解：（1）∵每个班之间间隔2米，如图所示，长方形场地长为b米，宽为a米，∴六个班级所占场地面积为：（b﹣4）（a﹣2）=（ab﹣4a﹣2b +8）平方米；
（2）根据题意得：18（b﹣4）=
×20×b，解得：b=36．故长方形的长b为36米．
浙大优学小学年级衔接捷径浙江大学出版社系列答案
【题目】某市制药厂需要紧急生产一批药品，要求必须在12天（含12天）内完成．为了加快生产，车间采取工人加班，机器不停的生产方式，这样每天药品的产量y（吨）是时间x（天）一次函数，且满足表中所对应的数量关系．由于机器负荷运转产生损耗，平均生产每吨药品的成本P（元）与时间x（天）的关系满足图中的函数图象．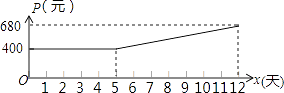 
时间x（天） | 2 | 4 |
每天产量y（吨） | 24 | 28 |
（1）求药品每天的产量y（吨）是时间x（天）之间的函数关系式；
（2）当5≤x≤12时，直接写出P（元）与时间x（天）的函数关系是P=；
（3）若这批药品的价格为1400元/吨，每天的利润设为W元，求哪一天的利润最高，最高利润是多少？（利润=价格﹣成本）
（4）为了提高工人加班的津贴，药厂决定在（3）中价格的基础上每吨药品加价a元，但必须满足从第5天到第12天期间，每吨加价a后每天的利润随时间的增大而增大，直线写出a的最小值．
