题目内容
【题目】图1、图2是两张形状大小完全相同的方格纸,方格纸中的每个小正方形的边长均为1,线段AB、EF的端点均在小正方形的顶点上.
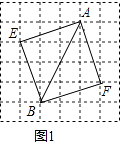
(1)如图1,作出以AB为对角线的正方形并直接写出正方形的周长; 
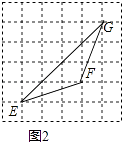
(2)如图2,以线段EF为一边作出等腰△EFG(点G在小正方形顶点处)且顶角为钝角,并使其面积等于4. 
【答案】
(1)解:以AB为对角线的正方形AEBF如图所示,正方形的周长为4 ![]() .
.
(2)解:等腰△EFG如图所示,S△EFG= ![]() ×
× ![]() ×
× ![]() =4.
=4.
【解析】(1)根据正方形的性质和判定,先画出图象,再根据勾股定理求出边长即可.(2)画等腰△EFG使得底边为4 ![]() ,高为
,高为 ![]() 即可解决问题.
即可解决问题.
【考点精析】关于本题考查的等腰三角形的性质和勾股定理的概念,需要了解等腰三角形的两个底角相等(简称:等边对等角);直角三角形两直角边a、b的平方和等于斜边c的平方,即;a2+b2=c2才能得出正确答案.

练习册系列答案
 励耘书业暑假衔接宁波出版社系列答案
励耘书业暑假衔接宁波出版社系列答案
相关题目













