��Ŀ����
����Ŀ�����ı���OABC�У�AB��OC��BC��x����C��A��1����1����B��3����1��������P��O���������x����������2����λ/����ٶ��˶�����P��PQ��OA��Q����P���˶���ʱ��Ϊt�루0��t��2������OPQ���ı���OABC�ص������ΪS��
��1����O��A��B����������ߵĽ���ʽ��ȷ������M�����ꣻ
��2���ú�t�Ĵ���ʽ��ʾP��Q��������ꣻ
��3������OPQ��P����ʱ����ת90�㣬�Ƿ����t��ʹ�á�OPQ�Ķ���O��Q�����������ϣ������ڣ�ֱ��д��t��ֵ���������ڣ���˵�����ɣ�
��4����S��t�ĺ�������ʽ��
���𰸡�
��1��
�⣺�������߹���A��1����1����B��3����1����
�������ߵĶԳ���Ϊֱ��x=2��
����������x�����һ����������Ϊ��4��0����
�������ߵĽ���ʽΪy=ax��x��4����
��A��1����1�������a1����3��=��1�����a= ![]() ��
��
�������ߵĽ���ʽΪy= ![]() x��x��4������y=
x��x��4������y= ![]() x2��
x2�� ![]() x��
x��
��y= ![]() ��x��2��2��
��x��2��2�� ![]() ��
��
�ඥ��M������Ϊ��2���� ![]() ����
����
��2��
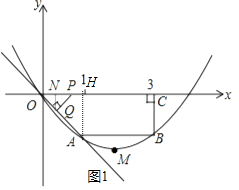
�⣺��QN��x����N��AH��x����H����ͼ1��
��A����1��1����
��OH=AH=1��
���AOHΪ����ֱ�������Σ�
���ONQΪ����ֱ�������Σ�
��QN=ON=NP= ![]() OP=t��
OP=t��
��P��2t��0����Q��t����t����
��3��
�⣺���ڣ�
��OPQ��P����ʱ����ת90��õ���O��PQ�䣬��ͼ2����Q��K��x����K��
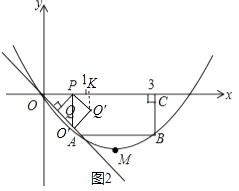
��QPQ��=90�㣬PO���x�ᣬPO��=PO=2t��PQ��=PQ= ![]() t����O�䣨2t����2t����
t����O�䣨2t����2t����
�ߡ�KPQ��=90�㩁��OPQ=45�㣬
�ߡ�PQ��KΪ���������Σ�
��PK=Q��k=t��
��Q�䣨3t����t����
��O�䣨2t����2t��������������ʱ����2t= ![]() 4t2��
4t2�� ![]() 2t�����t1=0��t2=
2t�����t1=0��t2= ![]() ��
��
��Q�䣨3t����t��������������ʱ����t= ![]() 9t2��
9t2�� ![]() 3t�����t1=0��t2=1��
3t�����t1=0��t2=1��
������������tΪ ![]() ��1ʱ��ʹ�á�OPQ�Ķ���O��Q�����������ϣ�
��1ʱ��ʹ�á�OPQ�Ķ���O��Q�����������ϣ�
��4��
�⣺��0��t��1ʱ����ͼ1��S= ![]() t2t=t��
t2t=t��
��1��t�� ![]() ʱ����ͼ3��PQ��AB��E�㣬S=S��POQ��S��AEQ=
ʱ����ͼ3��PQ��AB��E�㣬S=S��POQ��S��AEQ= ![]() t2t��
t2t�� ![]() ��t��1��
��t��1��
2��t��1��=2t��1��

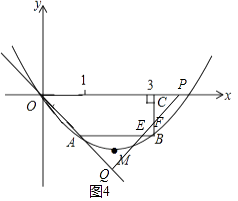
�� ![]() ��t��2����ͼ4��PQ��AB��E�㣬��BC��F�㣬
��t��2����ͼ4��PQ��AB��E�㣬��BC��F�㣬
�ߡ�POQΪ����ֱ�������Σ�
���CPF=45�㣬
���PCFΪ����ֱ�������Σ�
��PC=CF=2t��3��
��BF=1����2t��3��=4��2t��
��S��BEF= ![]() ��4��2t��2=2t2��8t+8��
��4��2t��2=2t2��8t+8��
��S=S����OABC��S��BEF= ![]() ��2+3��1����2t2��8t+8��=��2t2+8t��
��2+3��1����2t2��8t+8��=��2t2+8t�� ![]() ��
��
����������1�����öԳ��Եõ���������x�����һ����������Ϊ��4��0�������轻��ʽy=ax��x��4����Ȼ���A������������a���ɵõ������ߵĽ���ʽ���������䷽���õ�����M�����ꣻ��2����QN��x����N��AH��x����H����ͼ1�����ж���AOH�͡�ONQΪ����ֱ�������εõ�QN=ON=NP= ![]() OP=t��Ȼ����t��ʾ��P���Q�����ꣻ��3����OPQ��P����ʱ����ת90��õ���O��PQ�䣬��ͼ2����Q��K��x����K��������ת�����ʵá�QPQ��=90�㣬PO���x�ᣬPO��=PO=2t��PQ��=PQ=
OP=t��Ȼ����t��ʾ��P���Q�����ꣻ��3����OPQ��P����ʱ����ת90��õ���O��PQ�䣬��ͼ2����Q��K��x����K��������ת�����ʵá�QPQ��=90�㣬PO���x�ᣬPO��=PO=2t��PQ��=PQ= ![]() t����ȷ��O�䣨2t����2t����Q�䣨3t����t����Ȼ��ֱ��O�䣨2t����2t����Q�䣨3t����t�����������߽���ʽ�������Ӧ��t��ֵ����4�����ݡ�OPQ���ı���OABC�ص����ֵ�ͼ�β�ͬ�������ۣ���0��t��1ʱ���ص�����Ϊ�����Σ���ͼ1�����������������ʽ��ʾ��S����1��t��
t����ȷ��O�䣨2t����2t����Q�䣨3t����t����Ȼ��ֱ��O�䣨2t����2t����Q�䣨3t����t�����������߽���ʽ�������Ӧ��t��ֵ����4�����ݡ�OPQ���ı���OABC�ص����ֵ�ͼ�β�ͬ�������ۣ���0��t��1ʱ���ص�����Ϊ�����Σ���ͼ1�����������������ʽ��ʾ��S����1��t�� ![]() ʱ����ͼ3��PQ��AB��E�㣬�ص�����Ϊ���Σ���������������IJ��ʾS����
ʱ����ͼ3��PQ��AB��E�㣬�ص�����Ϊ���Σ���������������IJ��ʾS���� ![]() ��t��2����ͼ4��PQ��AB��E�㣬��BC��F�㣬�ص�����Ϊ����OABC��ȥ��BEF�����������ε������ȥ����������ɱ�ʾ��S��
��t��2����ͼ4��PQ��AB��E�㣬��BC��F�㣬�ص�����Ϊ����OABC��ȥ��BEF�����������ε������ȥ����������ɱ�ʾ��S��

 �������ͬ������ϵ�д�
�������ͬ������ϵ�д�






