题目内容
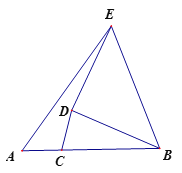
【题目】已知:如图,在半径为2的扇形![]() 中,
中,![]() °,点C在半径OB上,AC的垂直平分线交OA于点D,交弧AB于点E,联结
°,点C在半径OB上,AC的垂直平分线交OA于点D,交弧AB于点E,联结![]() .
.
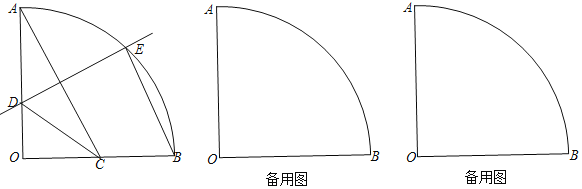
(1)若C是半径OB中点,求![]() 的正弦值;
的正弦值;
(2)若E是弧AB的中点,求证:![]() ;
;
(3)联结CE,当△DCE是以CD为腰的等腰三角形时,求CD的长.
【答案】(1)![]() ;(2)详见解析;(2)当
;(2)详见解析;(2)当![]() 是以CD为腰的等腰三角形时,CD的长为2或
是以CD为腰的等腰三角形时,CD的长为2或![]() .
.
【解析】
(1)先求出OC![]() OB=1,设OD=x,得出CD=AD=OA﹣OD=2﹣x,根据勾股定理得:(2﹣x)2﹣x2=1求出x,即可得出结论;
OB=1,设OD=x,得出CD=AD=OA﹣OD=2﹣x,根据勾股定理得:(2﹣x)2﹣x2=1求出x,即可得出结论;
(2)先判断出![]() ,进而得出∠CBE=∠BCE,再判断出△OBE∽△EBC,即可得出结论;
,进而得出∠CBE=∠BCE,再判断出△OBE∽△EBC,即可得出结论;
(3)分两种情况:①当CD=CE时,判断出四边形ADCE是菱形,得出∠OCE=90°.在Rt△OCE中,OC2=OE2﹣CE2=4﹣a2.在Rt△COD中,OC2=CD2﹣OD2=a2﹣(2﹣a)2,建立方程求解即可;
②当CD=DE时,判断出∠DAE=∠DEA,再判断出∠OAE=OEA,进而得出∠DEA=∠OEA,即:点D和点O重合,即可得出结论.
(1)∵C是半径OB中点,∴OC![]() OB=1.
OB=1.
∵DE是AC的垂直平分线,∴AD=CD.设OD=x,∴CD=AD=OA﹣OD=2﹣x.
在Rt△OCD中,根据勾股定理得:(2﹣x)2﹣x2=1,∴x![]() ,∴CD
,∴CD![]() ,∴sin∠OCD
,∴sin∠OCD![]() ;
;
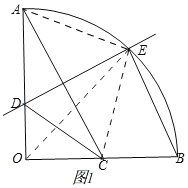
(2)如图1,连接AE,CE.
∵DE是AC垂直平分线,∴AE=CE.
∵E是弧AB的中点,∴![]() ,∴AE=BE,∴BE=CE,∴∠CBE=∠BCE.
,∴AE=BE,∴BE=CE,∴∠CBE=∠BCE.
连接OE,∴OE=OB,∴∠OBE=∠OEB,∴∠CBE=∠BCE=∠OEB.
∵∠B=∠B,∴△OBE∽△EBC,∴![]() ,∴BE2=BOBC;
,∴BE2=BOBC;
(3)△DCE是以CD为腰的等腰三角形,分两种情况讨论:
①当CD=CE时.
∵DE是AC的垂直平分线,∴AD=CD,AE=CE,∴AD=CD=CE=AE,∴四边形ADCE是菱形,∴CE∥AD,∴∠OCE=90°,设菱形的边长为a,∴OD=OA﹣AD=2﹣a.在![]() 2(舍)或a=
2(舍)或a=![]() ;∴CD=
;∴CD=![]() ;
;
②当CD=DE时.
∵DE是AC垂直平分线,∴AD=CD,∴AD=DE,∴∠DAE=∠DEA.
连接OE,∴OA=OE,∴∠OAE=∠OEA,∴∠DEA=∠OEA,∴点D和点O重合,此时,点C和点B重合,∴CD=2.
综上所述:当△DCE是以CD为腰的等腰三角形时,CD的长为2或![]() .
.

 七星图书口算速算天天练系列答案
七星图书口算速算天天练系列答案