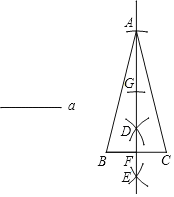题目内容
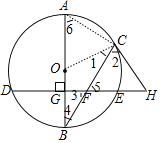
【题目】如图,![]() 为
为![]() 的直径,弦
的直径,弦![]() ,
,![]() 相交于点
相交于点![]() ,且
,且![]() 于点
于点![]() ,过点
,过点![]() 作
作![]() 的切线交
的切线交![]() 的延长线于点
的延长线于点![]() .
.
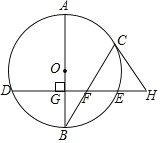
(1)求证:![]() ;
;
(2)若![]() 的半径为5,点
的半径为5,点![]() 是
是![]() 的中点,
的中点,![]() ,写出求线段
,写出求线段![]() 长的思路.
长的思路.
【答案】(1)见解析;(2)求解思路见解析.
【解析】
(1)连接OC,根据切线定理可知![]() ,根据
,根据![]() 得到
得到![]() ,利用同圆半径相等得到
,利用同圆半径相等得到![]() ,进而得到
,进而得到![]() ,再利用对顶角以及等量代换即可完成.
,再利用对顶角以及等量代换即可完成.
(2)思路一:①![]() 过圆心且点
过圆心且点![]() 是
是![]() 的中点,由垂径定理可得
的中点,由垂径定理可得![]() ,
,![]() ;
;
②由![]() 与
与![]() 互余,
互余,![]() 与
与![]() 互余可得
互余可得![]() ,从而可知
,从而可知![]() ;
;
③在![]() 中,由
中,由![]() ,可设
,可设![]() ,
,![]() ,由勾股定
,由勾股定
理,得![]() ,可解得
,可解得![]() 的值;
的值;
④由![]() ,可求
,可求![]() 的长.
的长.
思路二:连接![]() ,如图3.
,如图3.
①由![]() 是
是![]() 的直径,可得
的直径,可得![]() 是直角三角形,知
是直角三角形,知![]() 与
与![]() 互余,
互余,
又![]() 可知
可知![]() 与
与![]() 互余,得
互余,得![]() ;
;
②由![]() ,
,![]() ,可得
,可得![]() ,从而可知
,从而可知![]() ;
;
③在![]() 中,由
中,由![]() ,可设
,可设![]() ,
,
由勾股定理,得![]() ,可解得
,可解得![]() 的值;
的值;
④由![]() ,可求
,可求![]() 的长.
的长.
(1)证明:连接![]() ,如图1.
,如图1.
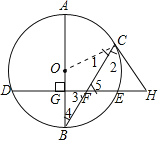
∵![]() 是
是![]() 的切线,
的切线,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,
∴![]() ,
,
又∵![]() ,
,
∴![]() ,
,
∴![]() .
.
(2)求解思路如下:
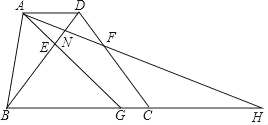
思路一:连接![]() ,如图2.
,如图2.
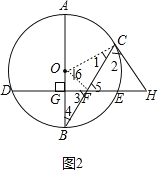
①![]() 过圆心且点
过圆心且点![]() 是
是![]() 的中点,由垂径定理可得
的中点,由垂径定理可得![]() ,
,![]() ;
;
②由![]() 与
与![]() 互余,
互余,![]() 与
与![]() 互余可得
互余可得![]() ,从而可知
,从而可知![]() ;
;
③在![]() 中,由
中,由![]() ,可设
,可设![]() ,
,![]() ,由勾股定理,得
,由勾股定理,得![]() ,可解得
,可解得![]() 的值;
的值;
④由![]() ,可求
,可求![]() 的长.
的长.
思路二:连接![]() ,如图3.
,如图3.
①由![]() 是
是![]() 的直径,可得
的直径,可得![]() 是直角三角形,知
是直角三角形,知![]() 与
与![]() 互余,
互余,
又![]() 可知
可知![]() 与
与![]() 互余,得
互余,得![]() ;
;
②由![]() ,
,![]() ,可得
,可得![]() ,从而可知
,从而可知![]() ;
;
③在![]() 中,由
中,由![]() ,可设
,可设![]() ,
,
由勾股定理,得![]() ,可解得
,可解得![]() 的值;
的值;
④由![]() ,可求
,可求![]() 的长.
的长.

练习册系列答案
 学习实践园地系列答案
学习实践园地系列答案
相关题目