题目内容
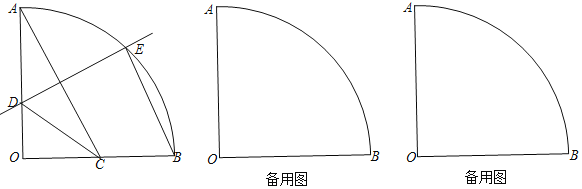
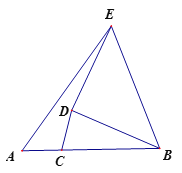
【题目】如图,已知线段AB=9,点C为线段AB上一点,AC=3,点D为平面内一动点,且满足CD=3,连接BD将BD绕点D逆时针旋转90到DE,连接BE、AE,则AE的最大值为 ________。
【答案】![]()
【解析】
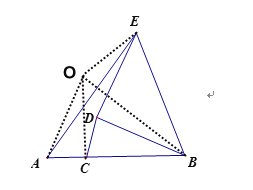
以BC为直角边在BC上方作等腰直角三角形BOC,如图,连接AO、OE.证明△EBO∽△DBC,从而发现E点运动的轨迹是以O为圆心,OE=![]() 为半径的圆,求出AO,最后根据三角形三边关系,可得AC最大值.
为半径的圆,求出AO,最后根据三角形三边关系,可得AC最大值.
解:以BC为直角边在BC上方作等腰直角三角形BOC,如图,连接AO、OE.
则![]() ,
,
∵∠EBD=∠OBC,
∴∠EBO=∠DBC,
∴△EBO∽△DBC.
∴![]() .
.
∵D点运动轨迹是以C为圆心,CD=3为半径的圆,
∴E点运动的轨迹是以O为圆心,OE=![]() 为半径的圆.
为半径的圆.
∵AE≤AO+OE,AO=![]() ,OE=
,OE=![]() .
.
∴AE最大值为:![]() .
.
故答案为:![]() .
.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
【题目】自1993年起,联合国将每年的3月22日定为“世界水日”,宗旨是唤起公众的节水意识,加强水资源保护.某校在开展“节约每一滴水”的活动中,从初三年级随机选出20名学生统计出各自家庭一个月的节约用水量,有关数据整理如下表.
节约用水量(单位:吨) | 1 | 1.2 | 1.4 | 2 | 2.5 |
家庭数 | 4 | 6 | 5 | 3 | 2 |
这组数据的中位数和众数分别是( )
A. 1.2,1.2; B. 1.4,1.2; C. 1.3,1.4; D. 1.3,1.2.